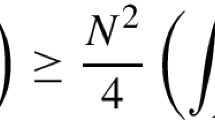1 Introduction

Open bounded sets in Euclidean space provide an important and well-studied instance of spectral geometry. Recently, discrete analogues of such sets have become a focus of attention [6, 10, 11]. In particular, Georgakopoulos et al. [6] propose the concept of canonically compactifiable graphs as graphs with strong intrinsic compactness properties. By definition, a graph is called canonically compactifiable if all functions of finite energy are bounded. For such graphs, there is a natural compactification, namely, the Royden compactification. Clearly, in order to study the geometry of such graphs, it is desirable to understand metric compactness features of such graphs.

As shown in [6], total boundedness with respect to common metrics such as the resistance metric or a standard length metric implies that the underlying graph is canonically compactifiable but the converse is not true. So, Georgakopoulos et al. [6] leave open the question of a metric compactness characterization of such graphs. Still, a candidate for such a characterization is proposed there. More specifically, it is shown that total boundedness with respect to all finite measure intrinsic metrics implies that the graph is canonically compactifiable and the converse is shown to hold for locally finite trees. The converse for general graphs, however, remained open and is posed as a problem in [6]. The first main result of this note (Theorem 1) solves this problem. Combining this main result with the mentioned result of Georgakopoulos et al. [6], we obtain that a graph is canonically compactifiable if and only if it is totally bounded with respect to all metrics that are intrinsic with respect to a finite measure (Corollary 1). This characterization turns out to extend without modification to general (non connected) graphs.

To put this result in perspective, we briefly discuss the relevance of intrinsic metrics next. Intrinsic metrics for strongly local Dirichlet forms were introduced in [18] and have subsequently played a fundamental role as they allow for a study of intrinsic spectral geometry of such forms. For general regular Dirichlet forms, a concept was only proposed recently in [5] (see [3, 4, 7, 19] for independent related studies on graphs). A special feature of the case of general Dirichlet forms is well worth pointing out: While in the strongly local case there is a maximal intrinsic metric, there are, in general, several incomparable intrinsic metrics on graphs [5]. Hence, in general, one cannot expect that it will be sufficient to consider only one intrinsic metric for graphs. Recent years have witnessed rather successful applications of intrinsic metrics in order to understand spectral geometry of graphs, see the mentioned works as well as, e.g., [1, 2, 8]. Given this, it is very natural to look for a characterization of the intrinsic compactness property of canonical compactifiability in terms of intrinsic metrics. Theorem 1 provides such a characterization.

In the last section, we provide an answer to another question raised in [6]. This question concerns an algebraic characterization of canonically compactifiable graphs. More specifically, in [6], it is shown that the set of functions of finite energy is an algebra if the graph is canonically compactifiable and we show that the converse is also true (Theorem 2). Our proof can be modified slightly to obtain a similar characterization for uniform transience (Theorem 3), a property that was recently introduced in [10]. Moreover, it can also be generalized to resistance forms in the sense of Kigami [12]. We briefly discuss this extension in Theorem 4. Typical examples for resistance forms are provided by metric graphs and fractals, we refer to [12, 13] for details.

2 Background

In this section, we first introduce the necessary notations and recall basic facts shown in [6] (see [9] for a description of the general setting as well).

A weighted graph \(G=(X,b)\) consists of a nonempty countable set X of nodes and a symmetric edge weight function \(b: X\times X \rightarrow [0,\infty )\) that vanishes on the diagonal and satisfies the summability condition

$$\begin{aligned} \sum \limits _{y\in X} b(x,y) < \infty \ \mathrm {for\ all\ } x\in X. \end{aligned}$$

Two nodes \(x,y\in X\) are called connected if there is a sequence \((x=x_0,\ldots ,x_n=y)\) with \(b(x_k,x_{k+1}) > 0\) for all \(0\le k < n\). Similarly, a graph is called connected if all of its nodes are connected.

This graph structure gives rise to a quadratic form that assigns to any function \(f:X\rightarrow {\mathbb {C}}\) its Dirichlet energy

$$\begin{aligned} {\tilde{Q}}(f) := \frac{1}{2}\sum \limits _{x,y\in X} b(x,y)|f(x)-f(y)|^2 \end{aligned}$$

and consequently defines the functions of finite energy

$$\begin{aligned} {\mathfrak {D}}(G) := \{f:X\rightarrow {\mathbb {C}} \mid {\tilde{Q}}(f) < \infty \}. \end{aligned}$$

This set is closed with respect to addition since

$$\begin{aligned} {\tilde{Q}}(f+g)^{1/2} \le {\tilde{Q}}(f)^{1/2} + {\tilde{Q}}(g)^{1/2}. \end{aligned}$$

The graph (X, b) is called canonically compactifiable if all functions of finite energy are bounded, that is if \({\mathfrak {D}}(G) \subseteq \ell ^\infty (X)\).

In the rest of this note, we will only look at connected graphs. We can do this since a graph is canonically compactifiable if and only if it has finitely many connected components (i.e. equivalence classes with respect to connectedness) and every connected component is canonically compactifiable. We will explicitly state if we don’t use this assumption.

For any \(o\in X\), we define a pseudo-norm \(\Vert \cdot \Vert _o\) on \({\mathfrak {D}}(G)\) via

$$\begin{aligned} \Vert f\Vert _o^2 := {\tilde{Q}}(f) + |f(o)|^2. \end{aligned}$$

Since we assumed connectedness, this yields a Hilbert space \(({\mathfrak {D}}(G), \Vert f\Vert _o)\) and the pointwise evaluation

$$\begin{aligned} {\mathfrak {D}}(G) \rightarrow {\mathbb {C}}, \qquad f\mapsto f(x), \end{aligned}$$

is continuous for every \(x\in X\), see, e.g., [15, Section 1.2].

Pseudo metrics are symmetric functions \(\sigma : X\times X\rightarrow [0,\infty )\) that vanish on the diagonal and satisfy the triangle inequality \(\sigma (x,z)\le \sigma (x,y) + \sigma (y,z)\).

Any pseudo metric \(\sigma \) naturally induces a distance from any nonempty subset \(U\subseteq X\) via

$$\begin{aligned} \sigma _U: X\rightarrow [0,\infty ),\qquad \sigma _U(x) = \inf \limits _{y\in U} \sigma (x,y), \end{aligned}$$

and the diameter of \(U\subseteq X\) by

$$\begin{aligned} \mathrm {diam}_\sigma (U) := \sup \limits _{x,y \in U} \sigma (x,y). \end{aligned}$$

Whenever (X, b) is a graph and m is a measure on X (i.e. an additive function \({\mathcal {P}}(X)\rightarrow [0,\infty ]\) induced by a node weight function \(X\rightarrow (0,\infty )\)), a pseudo metric \(\sigma \) is called intrinsic with respect to the measure m if the inequality

$$\begin{aligned} \frac{1}{2}\sum \limits _{y\in X} b(x,y)\sigma (x,y)^2 \le m(\{x\}) \end{aligned}$$

holds for all \(x\in X\).

Any graph (X, b) comes with a metric \(\varrho \) defined as

$$\begin{aligned} \varrho (x,y):=\sup \left\{ |f(x)-f(y)| \mid f\in {\mathfrak {D}}(G)\ \mathrm {with}\ {\tilde{Q}}(f) \le 1\right\} . \end{aligned}$$

Given this definition, it is easy to see that any function f of bounded Dirichlet energy satisfies

$$\begin{aligned} |f(x)-f(y)| \le {\tilde{Q}}(f)^{1/2} \varrho (x,y). \end{aligned}$$

Indeed, the inequality is optimal; the definition of \(\varrho \) gives that it is characterized by

$$\begin{aligned} \inf \{{\tilde{Q}}(f)\mid |f(x) - f(y)| = C\} = \frac{C^2}{\varrho (x,y)^2} \end{aligned}$$

for any \(C>0\). The metric \(\varrho \) is tied to canonical compactifiability, as [6, Theorem 4.3] proves that a connected graph (X, b) is canonically compactifiable if and only if it is bounded with respect to \(\varrho \), i.e. \(\mathrm {diam}_\varrho (X) < \infty \). This will be used below.

Remark

This metric is closely tied to the resistance metric r by \(\varrho ^2 = r\) (it is shown that r is a metric for locally finite graphs in [6, Theorem 3.19] and for general graphs in [14]). The metric is also related to intrinsic metrics (see [6, Theorem 3.13]).

Remark

Let us emphasize that our results do not assume local finiteness of the graph.

3 Characterization via intrinsic metrics

In this section, we provide a characterization of canonical compactifiability via intrinsic pseudo metrics.

A key step is the subsequent lemma. It provides an estimate for the energy of the distance to a set with respect to an intrinsic pseudo metric, which may be of interest in other contexts as well. A different bound (by m(X) instead of \(2m(X\setminus U)\)) is given in [6, Propositions 3.10 and 3.11].

Lemma 1

Let \(G = (X,b)\) be a graph and let \(\sigma \) be an intrinsic pseudo metric with respect to a finite measure m on X. For a nonempty subset \(U\subset X\), the energy of \(\sigma _U\) is bounded by

$$\begin{aligned} {\tilde{Q}}(\sigma _U) \le 2 m(X\setminus U). \end{aligned}$$

Proof

Immediately, we deduce \(\sigma _U(x) = 0\) for all \(x\in U\) and \(|\sigma _U(x)- \sigma _U(y)|\le \sigma (x,y)\) for all \(x,y\in X\). These properties already imply the desired bound on the Dirichlet energy of \(\sigma _U\):

$$\begin{aligned} {\tilde{Q}}(\sigma _U)= & {} \frac{1}{2} \sum _{x,y} b(x,y) (\sigma _U(x) - \sigma _U(y))^2\\= & {} \frac{1}{2} \sum _{(x,y) \in X^2\setminus U^2} b(x,y) (\sigma _U(x) - \sigma _U(y))^2\\\le & {} \frac{1}{2} \sum _{(x,y) \in X^2\setminus U^2} b(x,y) \sigma (x,y)^2\\= & {} \sum _{x\in X\setminus U} \left( \frac{1}{2} \sum _{y\in X} b(x,y) \sigma (x,y)^2\right) + \sum _{y\in X\setminus U} \left( \frac{1}{2} \sum _{x\in U} b(x,y) \sigma (x,y)^2\right) \\\le & {} 2 m (X\setminus U). \end{aligned}$$

Here, we used the fact that \(\sigma \) is intrinsic with respect to m in the last estimate.

\(\square \)

Theorem 1

Let (X, b) be a canonically compactifiable graph and consider a pseudo metric \(\sigma \) which is intrinsic with respect to a finite measure m. Then (X, b) is totally bounded with respect to \(\sigma \).

Proof

Fix an arbitrary \(\varepsilon > 0\). We have to find a finite subset S of X with \(\sigma _S (x) < \varepsilon \) for all \(x\in X\).

For \(\delta > 0\), define the set \(U_\delta = \{x\in X: m(\{x\}) < \delta \}\). As m is finite and the graph is canonically compactifiable (i.e. \(\mathrm {diam}_\varrho (X) < \infty \) holds by [6, Theorem 4.3]), we can choose \(\delta > 0\) such that

$$\begin{aligned} m(U_\delta ) < \frac{\varepsilon ^2}{2\ \mathrm {diam}_\varrho (X)^2}. \end{aligned}$$

We now claim that the set \(S:=X\setminus U_\delta \) has the desired properties:

Indeed, the set is finite as we clearly have \(|S| \le \frac{m(X)}{\delta } < \infty \).

Moreover, \(\sigma _S(x) < \varepsilon \) can be proven as follows: Lemma 1 helps us to estimate the Dirichlet energy of the function \(\sigma _S\):

$$\begin{aligned} {\tilde{Q}}(\sigma _S)\le & {} 2 m (U_\delta )\\< & {} \frac{\varepsilon ^2}{\mathrm {diam}_\varrho (X)^2}. \end{aligned}$$

Now, recall the inequality \(|f(x)-f(y)|\le {\tilde{Q}}(f)^{1/2}\varrho (x,y)\) and pick an arbitrary point \(o\in S\) to see

$$\begin{aligned} \sigma _S(x) = |\sigma _S(x) - \sigma _S(o)| \le {\tilde{Q}}(\sigma _S)^{1/2} \mathrm {diam}_\varrho (X) < \varepsilon . \end{aligned}$$

This finishes the proof. \(\square \)

Combining the previous theorem with its converse, [6, Corollary 4.5], and the fact that a general graph is canonically compactifiable if and only if it has finitely many connected components and each component is canonically compactifiable, we obtain the following characterization of canonically compactifiable graphs.

Corollary 1

A (not necessarily connected) graph (X, b) is canonically compactifiable if and only if X is totally bounded with respect to any pseudo metric \(\sigma \) that is intrinsic with respect to a finite measure.

4 Algebraic characterization

In this section, we will prove that a graph is canonically compactifiable if and only if the space of functions of finite energy is an algebra (with the usual pointwise addition and multiplication of functions). The proof can be transferred to show a similar algebraic characterization of uniform transience and can even be extended to resistance forms, see the discussion after Corollary 2.

Since [6, Lemma 4.8] already states that the space of functions of finite Dirichlet energy is an algebra if the underlying graph is canonically compactifiable, we will focus on the other direction.

Again, we use the splitting of canonical compactifiability to reduce the problem to connected graphs.

Theorem 2

Let \(G=(X,b)\) be a graph. If the space of functions of finite Dirichlet energy \({\mathfrak {D}}(G)\) is an algebra, the graph G is canonically compactifiable.

Proof

We analyze graphs that are not canonically compactifiable and find functions \(f\in {\mathfrak {D}}(G)\) such that \({\tilde{Q}}(f^2) = \infty \), implying that \({\mathfrak {D}}(G)\) cannot be an algebra.

Let G be a graph that is not canonically compactifiable and fix an arbitrary node \(o\in X\). We know that \(\varrho \) is unbounded on G since G is not canonically compactifiable, see [6, Theorem 4.3]. Select an infinite sequence of nodes \((x_n:n\in I \subseteq {\mathbb {N}})\) such that \(8^n<\varrho (x_n,o)\le 8^{n+1}\) (if there is no such \(x_n\) for a certain n, just omit this index). Now, we aim to find functions \(f_n\in {\mathfrak {D}}(G)\) that satisfy

$$\begin{aligned} f_n(o)=0, f_n(x_n) = 4^n, 0\le f_n\le 4^n, \text { and } {\tilde{Q}}(f_n)\le 4^{-n}. \end{aligned}$$

Such functions exist because

$$\begin{aligned} 8^n < \varrho (x_n,o) = \sup \{|f(x_n) - f(o)| \mid f \in {\mathfrak {D}}(G), {\tilde{Q}}(f)\le 1\} \end{aligned}$$

yields

$$\begin{aligned} \inf \{{\tilde{Q}}(f)\mid f(o)=0, f(x_n) = 4^n, 0\le f\le 4^n\} = \frac{(4^n)^2}{\varrho (x_n,o)^2} < 4^{-n}, \end{aligned}$$

where the additional condition \(0\le f\le 4^n\) can be introduced since \({\tilde{Q}}\) is Markovian, i.e. \({\tilde{Q}}(0\vee f \wedge 4^n)\le {\tilde{Q}}(f)\) for all f.

Considering \(\sum \nolimits _{n\in I}{\tilde{Q}}(f_n)^{1/2} \le \sum \nolimits _{n=1}^{\infty } 2^{-n} = 1\) and the fact that \(({\mathfrak {D}}(G), \Vert \cdot \Vert _o)\) is a Hilbert space, the function \(f:= \sum \nolimits _{n\in I} f_n \in {\mathfrak {D}}(G)\) is well-defined and \({\tilde{Q}}(f)\le 1\). Conversely, for all \(n\in I\), we have

$$\begin{aligned} {\tilde{Q}}(f^2) \ge \frac{|f(x_n)^2 - f(o)^2|^2}{\varrho (x_n,o)^2} \ge \frac{f_n(x_n)^4}{\varrho (x_n,o)^2}\ge \frac{256^n}{64^{n+1}} = 4^{n-3}, \end{aligned}$$

thus \({\tilde{Q}}(f^2)=\infty \). \(\square \)

Combining Theorem 2 with its converse, [6, Lemma 4.8], then yields the following characterization.

Corollary 2

A graph \(G=(X,b)\) is canonically compactifiable if and only if the space of functions of finite Dirichlet energy \({\mathfrak {D}}(G)\) is an algebra.

Let \({\mathfrak {D}}_0(G)\) be the closure of \(C_c(X)\) in the Hilbert space

$$\begin{aligned} ({\mathfrak {D}}(G), \Vert \cdot \Vert _o) \end{aligned}$$

and define the metric

$$\begin{aligned} \varrho _0(x,y) = \sup \left\{ |f(x)-f(y)| \mid f\in {\mathfrak {D}}_0(G)\ \mathrm {with}\ {\tilde{Q}}(f) \le 1\right\} . \end{aligned}$$

The graph G is called uniformly transient if \({\mathfrak {D}}_0(G) \subseteq C_0(X)\), where \(C_0(X)\) stands for the closure of \(C_c(X)\) in \(\ell ^\infty (X)\), see [10, Section 2]. Moreover, for connected graphs, uniform transience is equivalent to the boundedness of \(\varrho _0\), see [10, Theorem 3.2].

The space \({\mathfrak {D}}_0(G) \cap \ell ^\infty (X)\) is an algebra, see [17, Theorem 6.2], and the proof of Theorem 2 can be modified by replacing \({\mathfrak {D}}(G)\) with \({\mathfrak {D}}_0(G)\) and \(\varrho \) with \(\varrho _0\). These observations yield the following characterization of uniform transience.

Theorem 3

A graph is uniformly transient if and only if \({\mathfrak {D}}_0(G)\) is an algebra.

The same line of reasoning also applies to resistance forms in the sense of Kigami. Here we only state the result and sketch a proof. For notation, further background, and examples, we refer to [12, 13].

Let \(({\mathcal {E}}, {\mathcal {F}})\) be a resistance form on the set \(X \ne \emptyset \), see [12, Definition 2.3.1], and let

$$\begin{aligned} \varrho _{{\mathcal {E}}}(x,y) = \sup \{|f(x) - f(y)| \mid f \in {\mathcal {F}}, {\mathcal {E}}(f) \le 1\} \end{aligned}$$

be the square root of the associated resistance metric. Our main result for resistance forms reads as follows.

Theorem 4

The following assertions are equivalent.

  1. (i)

    \({\mathcal {F}} \subseteq \ell ^\infty (X)\).

  2. (ii)

    \(\rho _{{\mathcal {E}}}\) is bounded.

  3. (iii)

    \({\mathcal {F}}\) is an algebra.

Proof

The equivalence of (i) and (ii) can be proven along the same lines as [6, Theorem 4.3].

  • (i) \(\Longrightarrow \) (iii): This follows from the fact that \({\mathcal {F}} \cap \ell ^\infty (X)\) is an algebra, see, e.g., [16, Theorem 2.22] and the following remark.

  • (iii) \(\Longrightarrow \) (ii): This can be proven along the same lines as Theorem 2. \(\square \)