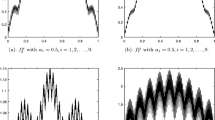Abstract
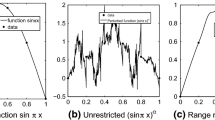
The fractal interpolation function (FIF) is a special type of continuous function on a compact subset of \({\mathbb{R}}\) interpolating a given data set. They have been proved to be a very important tool in the study of irregular curves arising from financial series, electrocardiograms and bioelectric recording in general as an alternative to the classical methods. It is well known that Jacobi polynomials form an orthonormal system in \({\mathcal{L}^{2}(-1,1)}\) with respect to the weight function \({\rho^{(r,s)}(x)=(1-x)^{r} (1+x)^{s}}\), \({r > -1}\) and \({s > -1}\). In this paper, a fractal Jacobi system which is fractal analogous of Jacobi polynomials is defined. The Weierstrass type theorem providing an approximation for square integrable function in terms of \({\alpha}\)-fractal Jacobi sum is derived. A fractal basis for the space of weighted square integrable functions \({\mathcal{L}_{\rho}^{2}(-1,1)}\) is found. The Fourier–Jacobi expansion corresponding to an affine FIF (AFIF) interpolating certain data set is considered and its convergence in uniform norm and weighted-mean square norm is established. The closeness of the original function to the Fourier–Jacobi expansion of the AFIF is proved for certain scale vector. Finally, the Fourier–Jacobi expansion corresponding to a non-affine smooth FIF interpolating certain data set is considered and its convergence in uniform norm and weighted-mean square norm is investigated as well.
Similar content being viewed by others
References
Agakhanov S.A., Natanson G.I.: The approximation of functions by the Fourier–Jacobi sums. Dokl. Akad. Nauk. 166, 9–10 (1996)
Barnsley M.F.: Fractal functions and interpolation. Constr. Approx. 2(4), 303–329 (1986)
Barnsley M.F.: Fractal Everywhere. Academic Press, San Diego (1988)
Barnsley M.F.: The calculus of fractal interpolation functions. J. Approx. Theory 57, 14–34 (1989)
Barnsley M.F., Elton J., Hardin D., Massopust P.: Hidden variable fractal interpolation functions. SIAM J. Math. Anal. 20(5), 1218–1242 (1989)
Belenkii A.M.: Uniform convergence of the FouriervJacobi series on the orthogonality segment. Math. Notes 46, 901–906 (1989)
Berezansky, Y.M., Kalyuzhnyi, A.A.: Harmonic Analysis in Hypercomplex Systems. Mathematics and Its Applications, Springer (2010)
Carothers N.L.: A Short Course on Banach Space Theory. London Mathematical Society Student Texts, Cambridge (2004)
Chand A.K.B., Kapoor G.P.: Generalized cubic spline fractal interpolation functions. SIAM J. Numer. Anal. 44, 655–676 (2006)
Chand A.K.B., Kapoor G.P.: Smoothness analysis of coalescence hidden variable fractal interpolation functions. Int. J. Nonlinear Sci. 3(1), 15–26 (2007)
Chand A.K.B., Navascues M.A.: Natural bicubic spline fractal interpolation. Nonlinear Anal. 69, 3679–3691 (2008)
Chand A.K.B., Navascues M.A.: Generalized Hermite fractal interpolation. Rev. R. Acad. Cienc. Exactas Ffs. Qufm. Nat. Zaragoza. 64(2), 107–120 (2009)
Cheney E.: Approximation Theory. AMS, Providence (1966)
Daugavet, I.K.: Introduction to Function Approximation Theory. Leningrad State University (1977)
Heil, C.: A Basis Theory Primer. In: Appl. Numer Harm. Analysis. Birkhauser, Boston (2011)
Higgins J.R.: Completeness and Basis Properties of Sets of Special Functions. University Press, Cambridge (1977)
Johnson D., Johnson J.: Low-pass filters using ultraspherical polynomials. IEEE Trans. Circuit Theory 13, 364–369 (1966)
Kvernadze G.: Uniform convergence of Fourier–Jacobi series. J. Approx. Theory 117, 207–228 (2002)
Motornyi V.P., Goncharov S.V., Nitiema P.K.: On the mean convergence of Fourier–Jacobi series. Ukr. Math. J. 62(6), 943–960 (2010)
Navascues M.A.: Fractal polynomial interpolation. Z. Anal. Anwend 25, 401–418 (2005)
Navascues M.A.: Fractal trigonometric approximation. Electron Trans. Numer. Anal. 20, 64–74 (2005)
Navascues M.A.: Non-smooth polynomials. Int. J. Math. Anal. 1, 159–174 (2007)
Navascues M.A.: Fractal interpolants on the unit circle. Appl. Math. Lett. 21(4), 366–371 (2008)
Navascues M.A.: Fractal approximation. Complex Anal. Oper. Theory 4, 953–974 (2010)
Navascues M.A.: Reconstruction of sampled signals with fractal functions. Acta Appl. Math. 110(3), 1199–1210 (2010)
Navascues M.A.: Fractal Haar system. Nonlinear Anal. 74(12), 4152–4165 (2011)
Navascues M.A.: Fractal bases of \({\mathcal{L}^{p}}\) spaces. Fractals 20(2), 141–148 (2012)
Navascues M.A., Chand A.K.B.: Fundamental sets of fractal functions. Acta Appl. Math. 100(3), 247–261 (2008)
Navascues, M.A., Sebastian, M.V.: Smooth fractal interpolation. J. Inequal. Appl. 1–20 (2006)
Navascues M.A., Sebastian M.V.: Legendre transform of sampled signals by fractal methods. Monogr. Mat. Garcfa Galdeano. 37, 181–188 (2012)
Pavlovic V.D.: Least-Square low-pass filters using Chebyshev polynomials. Int. J. Electroni. 53(4), 371–379 (1982)
Prasad J., Hayashi H.: On the uniform convergence of Fourier–Jacobi series. SIAM J Numer. Anal. 10(1), 23–27 (1973)
Suetin, P.K.: Classical Orthogonal Polynomial. 2nd rev. edn. Nauka, Moscow (1979)
Szego, G.: Orthogonal Polynomial, vol. 23. AMS Colloquium Publications (2003)
Viswanathan P., Chand A.K.B.: \({\alpha}\)-fractal rational splines for constrained interpolation. Electron Trans. Numer. Anal. 41, 1–23 (2014)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Akhtar, M.N., Guru Prem Prasad, M. & Navascués, M.A. Fractal Jacobi Systems and Convergence of Fourier–Jacobi Expansions of Fractal Interpolation Functions. Mediterr. J. Math. 13, 3965–3984 (2016). https://doi.org/10.1007/s00009-016-0727-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00009-016-0727-3