Fractal-Based Computational Modeling and Shape Transition of a Hyperbolic Paraboloid Shell Structure

Abstract

The concept of Takagi–Landsberg’s fractal surface is applied in this paper for constructing a parametric model of a hyperbolic paraboloid (hypar) shell structure using the Midpoint Displacement Method (MDM) based on the Iterated Function System (IFS) and controlled by the relative size value (w), a factor of fractal dimension. This method of generating a parametric model of a hypar is applied to create a domain of non-integer dimensions through which the hypar surface passes through textural changes, thus transforming the smooth hypar surface from its two-dimensional shape to a higher but non-integer-dimensional irregular surface that results in the changes of structural behavior. This paper briefly compares the structural behavior between the regular hypar and the fractal-based irregular hypar, and also searches the optimal shape of the hypar in terms of minimum deformation from the collection of its regular version and its different levels of irregular versions.

Introduction

Background and Problem Statement

At the beginning of the 20th century, thanks to the wide and efficient applications of reinforced cement concrete (RCC) technology, a number of shape-resistant or surface-active freeform shell structures started to appear. Since this period, RCC allowed architects and engineers to have more liberty to experiment with geometries in order to construct aesthetically new and elegant forms that are structurally efficient. The idea was to derive strength in a structure not just from the mass but from the shape itself. With this motivation, different mathematical surfaces were used as structural forms. The hyperbolic paraboloid is one of the most popular mathematical surfaces that have been prevalently used in designing thin concrete shells. Although, it is considered that Fernand Aimond (1902–1984) used hyperbolic paraboloids for constructing thin hypar concrete shells for the first time, it is Felix Candella (1910–1997) who is credited for popularizing this shape as a freeform, as well as in complex reinforced concrete shell structures, especially in the 1950s and 1960s (Faber 1963). Commonly a hyperbolic paraboloid is known as ‘HP’ or ‘hypar’, which is how the present paper will refer to it.

Geometrically, hypar is a doubly ruled quadratic surface that can be formulated by the following quadratic equation.

$$ z = \frac{{y^{2} }}{{a^{2} }} - \frac{{x^{2} }}{{b^{2} }} $$

(1)

The quadratic equation (Eq. 1) is a common choice for modeling a hypar at the early design stage in architecture. This equation allows designers to adjust the parameters (x, y, a, and b) for getting a desirable shape, size, slope and other form variations of the hypar. The ‘ruled surface generation’ method is also an easy alternative method for modeling a hypar (Maden et al. 2015). In this method, two main parameters l (directrix) and β (a measure of curvature) generate the width (b) and the height (h) of a hypar using the following relations:

$$ h = l \cdot \sin \beta $$

(2)

$$ b = l \cdot \cos \beta $$

(3)

The above relations (Eqs. 2, 3) also allow designers to obtain a parametric hypar that can be morphed by changing the values of l and β.

The key advantage of using the doubly ruled quadratic surface of a hypar for constructing a shell structure is the flexibility of manual and digital modeling as well as the ease of physical construction apart from its structural efficiency. Hypars are a saddle-shaped anticlastic surface which has two opposite curvatures and a series of straight lines can be drawn on this free-form saddle surface. Therefore, in construction, only linear members are required to make the scaffolding for constructing the curved surface. Structurally, the compression follows the convex curvature of a hypar while the tensions follow its concave curvature.

Using Eqs. (1), (2), and (3) for modeling a hypar, its different form-variations are created by morphing its basic shape. Sometimes, multiple hypars as segments are assembled in order to create architecturally unique appearances of freeform and joined shell structures without compromising their structural and constructional advantages. However, this approach of morphing a hypar has one limitation. That is, all the resulting morphed hypars are smooth in texture, which means the above methods are unable to obtain the hypar-derived form-variations beyond its smooth surface. On the contrary, Mandelbrot showed the Archimedes’ approach of Midpoint Displacement Method (MDM) for creating a smooth hypar which is controlled by the factor of relative size value (Mandelbrot 2002). The changing value of this unique geometric factor eventually changes the texture of the hypar surface from its smooth profile to a textured or folded profile. Therefore, the MDM method is able to produce different variations of smooth hypar as well as the hypars with a multiple levels of unsmoothness. This wide collection of smooth and unsmooth hypars may offer us architecturally innovative appearances of hypars, and perhaps reveal optimal or suboptimal hypars in its textured version instead of its smooth version. This quest for form-making and form-finding motivates this paper to explore different texture-based hypar variations and find the optimal or suitable variation among them.

Hypar, Geometric Dimensions and the Fractal Possibility

A regular hypar is a two-dimensional surface which is smooth and continuous. Most of the basic structural forms and their elements in architecture follow one-dimensional, two-dimensional and/or three-dimensional geometries. In other words, mostly their geometric dimensions are integer values. But in the Metric space and in nature, there exists other forms which possess non-integer dimensions. These forms are generally irregular, unsmooth and sometimes repetitive at different zooming scales. In short, they are broken at different hierarchical scales. Mandelbrot named these types of forms fractals (Mandelbrot 1983).

According to the concept of fractal geometry, one shape having certain integer-dimension can be transformed into another form of a higher or lower integer dimension (Mandelbrot 2002). For example, a two-dimensional surface ‘A’ can be transformed into both a one-dimensional grid and a three-dimensional solid-like shape (Fig. 1). During this transition, the initial shape passes through a domain of non-integer values. That means, until it gets it’s higher or lower integer-dimensional shapes, different levels of its fractal versions (non-integer-dimensional versions) will be produced. This domain of fractal or non-integer-dimensional shapes is the core interest of this study. In this paper, the hypar shell is taken as a base structure, and its shape is transformed through a passage of non-integer dimensions towards its higher integer-dimension, that is 3.0. The object of this study is two-fold. First, developing a fractal-based unsmooth hypar as an innovative and uncommon structural form followed by studying the impact of the factor of geometric dimension on the structural behavior of the parametric hypar. Second, finding structurally optimal forms in terms of the lowest deformation of a hypar from the population of its fractal-based unsmooth versions.

Fig. 1

Geometric transformation from the two-dimensional surface (A) to both the one-dimensional grid and the three-dimensional solid-like profile through two different domains of non-integer-dimensional values. The shapes that reside in this non-integer valued domains are fractals

In nature, many different forms and patterns, such as trees and leaf veins, exhibit fractal-like character having non-integer-dimensional values apart from their idiosyncratic recursive patterns. This unique fractal-like configuration of tree branches and leaf veins are in fact the configurations apparently showing structural rationality, mechanical optimality and biological functionality (Rian and Sassone 2014a, b). A crumpled paper, a non-integer-dimensional shape (D_H ≈ 2.5) and an example of a random fractal, is stiffer than a two-dimensional flat paper (D_H = 2.0) (Rian and Asayama 2016). There are also other built and unbuilt examples that show the structural potency and rationality of the fractal-like or fractal-based structures in architecture (Asayama and Mae 2004; Huylebrouck and Hammer 2006; Rian and Sassone 2014a, b; Rian and Asayama 2016; Rian et al. 2018). These examples have motivated this paper’s quest for finding unique and optimal forms of a spatial structure from the domain of non-integer dimensions using hypar as a benchmark example. But why hypar? Fractal-based shape transition means the changing of geometric dimension that eventually results in changing the smooth surface to an unsmooth surface. This geometric behavior of fractal geometry can be applied in studying the changing structural behavior of a surface-active structure. In this regard, a hypar is one type of surface-active shell structure which derives its strength from its surface topology. But, if it is gradually morphed into a textured or a multi-folded surface then its doubly curved smooth structural system will be transformed into a folded-plate-like structural system within the family of shell structures. This changing of one shell type to another as a result of fractal-based morphogenesis obviously influences its structural behavior, and to understand this changing behavior is one of the core interests of this paper.

Fractal Geometry

A Brief Mathematical Definition of Fractal Geometry

A general definition of a fractal is a shape, figure or pattern that encapsulates the copies of itself at the infinitely different level of scales; which means it is recursively self-similar at every zoom level. According to Robert Devaney’s (1992) mathematical definition, a fractal is a subset of Rn (an n-dimensional metric space) which is self-similar and whose Hausdorff dimension, its fractal dimension, surpasses its topological dimension. In a simpler description, fractal shapes are non-integer-dimensional shapes which fall in between two successive integer dimensions, 0 < D_H < 1, or 1 < D_H < 2, or 2 < D_H < 3, where D_H is a fractal dimension. According to Barnsley’s (2004) depiction, a fractal is a union of self-similar or self-affine sets that lie in a metric space, and more precisely in the Hausdorff metric space. His contraction mapping theory indicates that a fractal is an attractor. It is a resulting figure in the limit state obtained from a set of infinite transformations ‘f_i’ and it is a unique non-empty compact set. The resulting fractal shape can be obtained by the “intersection” of all self-similar or self-affine subsets (Fig. 2).

Fig. 2

Koch curve, as an attractor which is an intersection of all self-similar subsets of ‘K₀’ after affine transformations of f₁ and f₂

Iterated Function System (IFS)

A fractal is formed by the repeating of the original shape, after a geometric transformation in the first step, and then repeating this process iteratively in the next steps for multiple times. This process of repetition leads to the production of a fractal shape which can be unpredictable and indeterministic. Nevertheless, in 1981, based on the Hutchinson’s (1981) operator, Barnsley (2014) developed a recursive system, which he called as the Iterated Function System (IFS) that can predict the end result of a fractal formation in a deterministic way.

In IFS, the shape as an output produced at the finite number of iterations (n) is,

$$ A_{n} = \mathop \cup \limits_{i = 1}^{m} f_{i} (A_{n - 1} ) $$

(4)

The above relation shows that the affine transformation ‘f’ is the key determinant for the attractor ‘A’. It can be represented as,

$$ f = \lambda \left[ {\begin{array}{*{20}c} {\mu_{1} } & 0 \\ 0 & {\mu_{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\cos \theta } & { - \sin \theta } \\ {\sin \theta } & {\cos \theta } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} a \\ b \\ \end{array} } \right] $$

(5)

where λ is the contractivity factor, μ₁ and μ₂ are the reflections along X-axis and Y-axis, θ is the angle of rotation, and a and b are the displacements along X-axis and Y-axis respectively.

Fractal Dimension (D_H)

Fractal dimension is a measure of how complex, unsmooth, irregular or detailed a figure is. It is a “fractured” dimension that lies in between two successive integer dimensions. For example, Sierpinski carpet (Fig. 1) has the fractal dimension 1.893 which means that the iteratively perforated surface is neither a two-dimensional grid nor a three-dimensional surface, but shows a tendency of being a two-dimensional surface. Based on the Barnsley’s (1988) contraction mapping theory, the fractal dimension, also known as the Hausdorff dimension of a fractal is linked to the contractivity factors by the following relation:

$$ \mathop \sum \limits_{i = 1}^{k} \lambda_{i}^{D} = 1 $$

(6)

where λ_i is a contractivity factor of transformation f_i and k is the number of transformations.

For example, the Koch curve, shown in Fig. 2, produces two self-similar copies of itself at each iteration. The contractivity factor of both the triangles is 1/√3. Its fractal dimension D can be calculated as follows using Eq. 6,

$$ {\text{i}} . {\text{e}}.,\quad \left( {1/\surd 3 } \right)^{D} + \left( {1/\surd 3} \right)^{D} = 1 $$

Therefore,

$$ D = \frac{\log (1/2)}{\log (1/\surd 3)} = 1.262 $$

(7)

Modeling of a Hypar Using Fractal Geometry

Midpoint Displacement Method (MDM)

The Midpoint Displacement Method (MDM) was developed in the third century BC by Archimedes (287–212 BC) for calculating the area of a ‘parabola segment’. He first drew a vertical line from the midpoint of the baseline towards the parabolic curve where it touches at a point. Then he connected this curve point to the endpoints of the baseline; thus, obtained the first triangle. The area of this triangle was the first approximation of the parabola segment that created two new smaller parabolic segments. Next, he repeated the same process in these two new parabolic segments. He continued this process iteratively until the original parabolic segment is visibly packed by many triangles (Fig. 3, top). In this iterative process, 2⁰, 2¹, 2², …, 2ⁿ number of triangles are generated at 1, 2, 3, …, n iterations. According to Archimedes’ proposition, the area of each smaller triangle is one-eighth of the area of its parent triangle (Bovill 1996). In modern mathematics, it is true because the smaller triangle has half the width and one-quarter of the height of its parent triangle (Fig. 3, bottom). Therefore, if the area of the first triangle is ‘T’, then the area of the parabola segment is,

$$ {\text{Area}} = T + 2^{1} \left( {\frac{T}{{8^{1} }}} \right) + 2^{2} \left( {\frac{T}{{8^{2} }}} \right) + \cdots $$

(8)

$$ {\text{i}} . {\text{e}} ., \quad {\text{Area}} = \left( {1 + \frac{1}{4} + \frac{1}{{4^{2} }} + \frac{1}{{4^{3} }} + \cdots } \right)T $$

(9)

Fig. 3

Archimedes’ midpoint displacement method (MDM); top—dissection of a parabola segment into infinitely many triangles using MDM; bottom—the sizes of the parent and child triangles

From the above Eq. (9) it can be observed that the sequence of displacement factors for the midpoint displacements to construct a parabola are (1/4)⁰, (1/4)¹, (1/4)², …, (1/4)^n` for n number of iterations in which 1/4 is the common factor. This common factor of displacement is known as the relative size value.

Takagi and Landsberg’s Generalization

Takagi (1901), a Japanese number theorist, replaced the sequence of (1/4)⁰, (1/4)¹, (1/4)², …, (1/4)^n` with the sequence of (1/2)⁰, (1/2)¹, (1/2)², …, (1/2)ⁿ. By doing so, an unexpected change was observed; the smooth curve of the parabola was transformed into a highly unsmooth and approximately self-similar curve, which was later known as Takagi curve. This curve is a unique example of a fractal curve. Takagi represented the mathematical formulation of the Archimedes and the Takagi curve using the Blancmange function as follows,

$$ {\text{For Archimedes'}}\,\,{\text{parabola}},\quad A\left( x \right) = \mathop \sum \limits_{n = 0}^{z} (1/4)^{n} s(2^{n} x) $$

(10)

$$ {\text{For Takagi curve}},\quad A\left( x \right) = \mathop \sum \limits_{n = 0}^{z} (1/2)^{n} s(2^{n} x) $$

(11)

Here, s(2ⁿx) is a ‘saw-teeth function’, $s\left( x \right) = \mathop {\text{min} }\nolimits_{n \in z} \left| {x - n} \right|$ is the distance from x to the nearest integer. Therefore, when the relative size value is 1/4 in the Eq. (10), then it produces Archimedes’ parabola, and when it is 1/2 then it produces Takagi curve (Eq. 11). Later, in the mid-twentieth century, George Landsberg generalized the Blancmange function by replacing the relative size value by w parameter where 1/2 ≤ w ≤ 1. This generalized function generates a curve whose texture is changeable and nowhere-differentiable but uniformly continuous (Tall 1982). However, this generalized curve, known as the Takagi–Landsberg curve, is categorized as a special example of a fractal curve which is parametric in nature. The Cartesian form of the Blancmange function is,

$$ A\left( x \right) = \mathop \sum \limits_{n = 0}^{z} (w)^{n} s(2^{n} x) .$$

(12)

Modeling of a Takagi–Landsberg Curve Using IFS

In this paper, the vector method is used to execute the midpoint displacements followed by Archimedes’ approach and guided by the Takagi–Landsberg’s generalization (Eq. 12). In this method, the midpoint of a straight line is displaced towards the global Z-axis by height δ, producing two new lines. The midpoints of these two new lines are further displaced by a height δ₁ along global Z-axis where δ₁ = w.δ and ‘w’ is a relative size value. This process is continued iteratively on each new lines using IFS in such a way that the displacement on the nth step, δ_n = w. δ_(n−1). This way the IFS-based MDM produces the parabolic curve (w = 0.25) and Takagi curve (w = 0.5) (Fig. 4). In this process, the iteration number (n) and the relative size value (w) are the key variables that make the curve parametric and control its texture. Figure 5 shows changing levels of the texture of the Landsberg–Takagi curve with the changing of w value.

Fig. 4

IFS-based MDM that produces the Takagi curve (top) when w = 0.5, the parabolic curve when w = 0.25 (bottom)

Fig. 5

Takagi–Landsberg curves after six iterations and their Fractal dimensions (D_H) with the changing of w value

Takagi–Landsberg Surface: Modeling of a Parametric Hypar

The two-dimensional counterpart of the Takagi–Landsberg curve is the Takagi–Landsberg surface. This surface can be modeled by starting with the midpoints displacements of each edge of a flat square surface including the displacement of its center using the IFS-based MDM followed by the Takagi–Landsberg’s generalized function. When w = 0.25, the surface becomes a paraboloid, and when, w = 0.5, the surface becomes unsmooth. Its generalized version can be called as the Takagi–Landsberg surface. If the center point of the surface is displaced upward along the global Z-axis then the surface becomes a positive Gaussian surface (Fig. 6, top), i.e., a paraboloid (w = 0.25) and its fractal versions (w > 0.25). But, if the center of the surface is displaced downwards along the same Z-axis, then the surface will become a negative Gaussian surface (Fig. 6, bottom) which is, in fact, a hyperbolic paraboloid, i.e., hypar (w = 0.25) and its fractal versions (w > 0.25).

Fig. 6

IFS-based iterative midpoint displacements that create a paraboloid (top row) and a hypar (bottom row)

Fractal Dimension and Relative Size Value

Dubuc (1989) calculated the fractal dimension (D_H) of the Takagi–Landsberg’s surface using the relative size value (w). According to his calculation,

$$ {\text{D}}_{\text{H}} = \frac{\log (8w)}{\log (2)};\quad {\text{for }}0.5 \, < w < \, 1 $$

(13)

In accordance with this relation, when 0.5 < w < 1.0, the D_H of the Takagi–Landsberg surface is a non-integer between 2.0 and 3.0, which confirms that the Takagi–Landsberg surface is mathematically a fractal. It indicates that the higher the value of D_H, the higher the unsmoothness of the surface. However, when the 0.25 ≤ w ≤ 0.5, then the D_H value becomes 2.0 which is an integer and constant. In this state, the Takagi–Landsberg surface is not a mathematical fractal; yet, in this domain, the smooth surface starts becoming unsmooth carrying the constant D_H value (2.0) with the increasing of w value. It clarifies that the Takagi–Landsberg surface is more responsive to w parameters than the parameters of the fractal dimension if we consider the complete domain of w = 0.25 to w = 1.0. Accordingly, this paper will consider w as the key variable instead of the fractal dimension for the parametric design and structural analyses of the hypar shell structure in the next sections. Figure 7 shows different variations of the parametric hypar based on different w and D_H values.

Fig. 7

Fractal-based hypars with different w values and their corresponding fractal dimensions

Architectural Application of the Fractal-Based Hypar

Hypar

Since the 1930s, hyperbolic paraboloids and their different joining compositions have been frequently used as shell or roof structures. The hypar shape offers numerous possibilities to architects and engineers for designing and constructing doubly curved thin shells because of its surface flexibility and easy constructability. A hypar can be structurally considered as a combination of a series of arches and hanging cables (hyperbolas), hence it experiences compression (along arches) and tensions (along chains) under its own weight (Fig. 8). One important characteristic of a hypar is that the forces as a result of a uniformly distributed load are the same across the entire surface. Hypars gain strength from their shapes rather than their mass. The curvature of the hypar shape reduces its buckling tendency in compression and hence they can achieve high stiffness. By being braced in two opposite directions they experience almost no bending. Because of these form-active stress behavior, hypars are also categorized as a surface-active structure. Having negligibly less moment, a reinforced concrete hypar roof therefore can be thinner than the conventional roofs covering the same area (Denny 2010).

Fig. 8

a, b Hypars are a combination of two sets of parabolas and hyperbolas; c principal stresses (tension along hyperbolas and compression along parabolas) in a hypar

Fractal-Based Hypar and its Shape Approximation

All the above geometric and structural characteristics are true if a regular hypar is generated using the quadratic equation. But a hypar developed by IFS-based MDM has different structural and constructional characteristics because of their unsmooth surface. The following sections will briefly study its unique structural behavior. However, regarding practical scenario, the fractal-based model having w > 0.5 has one drawback which is its recessed surfaces like pockets. Pockets will collect rainwater, snow or even dust which eventually can make the structure heavy and vulnerable. Therefore, an approximation of the model is necessary in order to minimize this problem. In this study, the approximation has been done by elevating the central depressions and thus minimizing its collection capacity. We tested the water draining behavior on small-scale 3D-printed models of both the original fractal-based hypar (w = 0.6) and its approximated hypar, and the result confirms the advantage of the approximated model (Fig. 9).

Fig. 9

Water drainage test on the 3D-printed original fractal-based hypar model and its approximated model

This approximation does not drastically change the surface texture of the original fractal-based model except the central longitudinal part. The parametric set up of the w-based shape morphogenesis has been kept the same for the approximated model too. Figure 10 shows the variations of the approximated model based on different w values. However, this approximation obviously changes the structural behavior of the model. To understand the different structural behaviors of the regular, fractal-based, and approximated hypars including a regular folded hypar, finite element analyses have been carried out by focusing on the maximum deflections and Von Mises stresses of the structures under the gravity and self-weight in the following sections.

Fig. 10

A parametric model of the fractal-based approximated hypar with respect to changing w value

Structural Model

The fractal-based approximated hypar obtained in the previous section has been adopted for designing an architectural shell structure in order to assess its structural behavior using finite element analysis. The span length at each side of the hypar model is taken as 10.0 m, while the maximum height is decided 8.0 m. This height is changeable depending on the value of deviation (s) which is a height factor for the midpoint displacements. Two different supports have been provided; one is the supports throughout the edges of the same sides and another is the supports at the lowest vertices of two downward sides. The analyses have been started with the structural comparison between the smooth hypar (w = 0.25, and D_H = 2.0) and fractal-based hypar (w = 0.6, and D_H = 2.26). The hypar of w = 0.6 has been selected because its Hausdorff fractal dimension is non-integer (D_H = 2.26). To make the geometric model into a finite element model for the analysis, the surface has been transformed into a mesh which consists of thin quadratic shell elements. All the overlapping nodes and shell elements are discarded. The material is reinforced concrete with 10 cm uniform thickness. Only the dead loads have been considered for the analysis.

Finite Element Analysis and Results

Finite element analysis has been performed on the parametric model four different models that are (a) smooth hypar (w = 0.25), (b) fractal-based unsmooth hypar (w = 0.6), (c) fractal-based approximated hypar (w = 0.6), and (d) folded hypar. Karamba (Clemens Preisinger⁾, a finite element solver component has been used for the analyses. It works in the Grasshopper (McNeel and Associates), a parametric modeling environment implemented in Rhinoceros3D modeling software. Karamba is able to give prompt feedback by interacting with the parametric model. For the analyses, both the supporting systems have been adopted to understand the structural behavior in both scenarios. In the supporting system 1, the minimum deformation has been observed in the smooth and folded hypars as compared to the fractal-based hypars (Fig. 11). The smooth hypar can be assumed as a series of parabolic arches because of the fixed supports on the edges. This is the reason each parabolic arch enjoys compression resulting no moments and no considerable deformations. However, the top parts of parabolic arches form an inverted parabola, which acts like a hanging cable, and therefore we notice the tension along this region (red areas in Fig. 11, the first row and the ‘Stress’ column). Similar action is also experienced in the regular folded hypar (Fig. 11, the last row). Here, each folds act like a folded arch, whereas its top region, parallel to the supported edge, experiences tension. On the other hand, the fractal-based hypar can be considered as an irregular folded-plate shell structure which has multi-directional fold-lines. Before approximation, the fractal-based hypar has the maximum deformation which is seen along the central region parallel to the supporting edge (Fig. 11, the second row). This deformation is due to the inward folds or high depression of this region. However, other regions manage to obtain the self-stiffness because of the assemblage of multiple folded-plates. In this situation, if we fix the problem of the central depression along the longitudinal direction, then the substantial deformation can be avoided. That is the reason, its fractal-based approximated version behaves better than the fractal-based hypar (Fig. 11, the third row and the ‘Displacement’ column). The approximated model also experiences tension along the central ridge parallel to the supporting edges which is roughly similar to the stress action of the smooth hypar (Fig. 11, the third row and the ‘Stress’ column). The possible reason for this similarity can be understood by assuming that the approximated hypar is a combination of irregular arches perpendicular to the supporting edges and the tips of these arches form a region of an inverted irregular cable which accommodates tension.

Fig. 11

Finite element analyses of four different hypars having the supporting system 1

Figure 12 shows the finite element analysis results when supporting system 2 is adopted. It shows that the maximum deflections in both the smooth and fractal-based hypars are noticed at corner areas. The blue shaded areas in both the hypars have negligible deflections participating in channeling the stresses towards the supports, while the corner areas experience the maximum degree of freedom and thus facing maximum displacements. In other words, the blue shaded areas are only surface-active and shape-resistant areas while the corner areas are unnecessary because they do not participate in carrying forces towards the supports, instead, they are effectively freely hanging. It confirms why the hypars supported on two lowest points usually take shapes like Hypar B and Hypar C (Fig. 13). But, if we architecturally prefer the maximum covered area with the minimum supports, then the Hypar A (Fig. 13) profile is a better choice, although structurally Hypar B and Hypar C are more efficient ones. If we accept this preference, then we find that the fractal-based hypar and its approximated model experience the least deflection as compared to the smooth and folded hypars (Fig. 12). In regular folds (Fig. 12, the last row), if the transverse edges of the folded plates are not stiffened then only their longitudinal edges will have supports served by the fold lines. In this situation, the fold angles of the support-less folded arches become unstable, thus they experience the maximum deflection (Red region of the Fig. 12, the last row and the ‘Displacement’ column). That is why, we see only the supported folded arches are very strong showing in blue shades while the remaining unsupported folded arches are under high deflection are shown in green to red shades.

Fig. 12

Finite element analyses of four different hypars having the supporting system 2

Fig. 13

Hypar A with the region in blue active in transferring stress to the supports, while the non-blue areas at corners are inactive, thus seemingly unnecessary. In such a supporting condition, we prefer Hypar B and Hypar C type shell structures

The fractal-based hypars are irregular folded-plate-like shell structures which have multiple fold-lines in multiple directions. Each fold-line acts as a beam or end diaphragm for the adjacent folded flat plates. This means, all the edges of each flat plate (except the flat plates along the free edges of the hypar) are stiffened by the fold-lines, and as a whole, the overall folded surface enjoys self-stiffness because of the fold-lines. This kind of folded surface thus resists flattening the surface. Hence, having supports on the lowest points (supporting system 2), the fractal-based hypars and their approximated versions are stiffer than the smooth hypar and the one-directional folded hypar. It is observed that the maximum deflections have occurred mainly at the corner areas. But if we discard the corner areas, then the corner-less smooth hypar performs stronger than the corner-less fractal-based hypars.

Search for the Optimal Hypars

The above comparison clarifies that the regular hypar is stiffer than the fractal-based approximated hypars for the all edge supporting system; supporting system 1. On the other hand, in the supporting system 2, the regular hypar has more deflection at corners than the fractal-based original and approximated hypars (w = 0.6). However, for finding an optimal form (in terms of lowest deformation) from the population of hypars having the w values ranging from 0.25 to 1.0, an optimization process has been performed for two different supporting systems by fixing the domain of w variable and height variable from 0.25 to 1.0 and from 7.0 to 10.0 m respectively. During this searching process, other structural factors, such as buckling, bending, cracking and stability, have been ignored to simplify the search process.

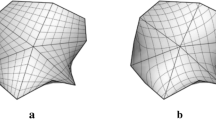
After ending the search at 100th generation, we found four different optimal outcomes for four different boundary conditions (Fig. 14). As expected, the smooth hypars have the lowest deflections for supporting system 1. The obvious reason is each transverse cross-section of a smooth hypar acts as a parabolic arch because of the full-edge supports whereas each transverse cross-section in the fractal-based irregular hypar is an irregular arch which is much weaker than the smooth parabolic arch. In both the cases. Having the full edge supports at both sides, bending is negligible in the smooth hypar while in the irregular hypar, a small amount of bending is developed although minimized by the folded-plate-like action. For the variable height condition, smooth hypar of 7.75 m height was found to be the optimal one in terms of having the lowest deformation, while for the fixed height, smooth hypar (8.0 m) is nearly as strong as the 7.75 m high hypar. In supporting system 2, the lowest deformations are noticed at the corners as usual. As the corner areas are structurally useless in the case of supporting system 2, if we discard the corner areas, then the optimality in terms of the lowest deformation, noticed at the tips of the free edges, is found in the smooth hypar (w = 0.25). But, because we prefer to have the maximum covered area with the minimum supports, then the corner areas are important to consider for the structural analysis and optimization. With this preference, we have found that the fractal-based approximated hypar having w = 0.75 (fractal dimension 2.59) and height 9.72 m has the lowest corner deformation for the varying height condition under the supporting condition 2, while the hypar with w = 0.85 (fractal dimension 2.77) under the same supporting system shows the lowest deflection for the fixed height condition.

Fig. 14

Optimal models of hypars in terms of the minimum deformation for four different boundary conditions

However, a relation between the maximum displacement (δ) with respect to w value give a clear picture of the relation between the degree of surface irregularity and the maximum deflection (Fig. 15, left). For the supporting system 1, the minimum deflection is seen at w = 0.25. Till the w = 0.5, the maximum deflection gets higher. But from w = 0.5 onwards, the maximum deflection gets slowly and gradually less till w = 1.0. In this shape morphogenesis, the regular hypar as a doubly curved structural system starts losing its shape-resistant quality once it crosses the w value at 0.5. After w = 0.5, the overall hypar is turned into a new structural system which is a folded-plate-like hypar shell. As w gets higher after w = 0.5, the folding density gets higher and folding angles get lower, and hence, the stiffness also gets higher. For the supporting system 2, the maximum deflection is noticed in the smooth hypar and the deflection gets lower as w value gets higher (Fig. 15, right). In this system, the corners of the smooth hypar experience heavy deformation because of high bending. When w value gets higher, the surface starts becoming irregular folds, and consequently, it starts generating self-stiffness. In this relation, we find the lowest deflection at w = 0.85.

Fig. 15

Relative size value (w) vs. displacement (δ) relation for the Supporting System 1 (Left) and Supporting System 2 (Right)

Constructability of the Fractal-Based Hypar

A smooth hypar is easy to construct because only a set of straight members is needed to create the form-work. However, in the case of the uneven fractal-based hypar, the foremost issue is the form-work preparation for such an irregular form. For selecting the construction material, reinforced concrete has been preferred instead of wood or steel to avoid the challenges of jointing the wooden or steel members. Reinforced concrete is also not difficult to caste on a prepared formwork; it is structurally monolithic and aesthetically expressive which can highlight the surface irregularity.

Geometrically, the fractal-based hypar’s Takagi–Landsberg surface is a rule-based complex form and it has a self-similar property which provides a hint of easy modular construction (Rian et al. 2018). Each cross-section of the fractal-based hypar along the longitudinal direction is a Takagi–Landsberg curve, and each curve at a unit distance is the same, only their base heights are different (Fig. 17a). It gives an easy solution. Each Takagi–Landsberg curve is in fact a resultant of triangles generated during the midpoint displacements (Fig. 4). It means these triangles can be made of wood and the assemblage of wooden triangles will become truss-like unit whose outer line is, in fact, the Takagi–Landsberg curve, i.e., an irregular arch and will act as a formwork module (Fig. 16). Each identical curve in the form of an irregular truss-like wooden arch as a self-similar module will be placed at each unit distance for making the scaffolding. It can be noticed that the bases of all arched units are actually the vertices of an inverted Takagi–Landsberg curve at each supporting side (Fig. 17a). This base at each supporting edge will be prepared by a steel frame (Fig. 17b). The trussed arch modules will be then placed on the prepared bases and connected to each other at their vertices by wooden laths (Fig. 17c) which will create a quadratic grid on the top. Thus, the formwork will eventually become a strong space-frame-like system which can carry the load of reinforced concrete during the casting. Next, each grid units on the top will be covered by a flat wooden panel. Additionally, another simple formwork will be prepared for creating the supporting system 2. When the final scaffolding is ready, the next process is laying 10 cm thick reinforced concrete. Later, all the scaffolding will be removed. Figure 18 shows an architectural impression of the final structure after removing the formwork.

Fig. 16

Front elevations. Left—geometric progression of making a trussed arch based on Takagi–Landsberg curve; right—the approximation of the trussed arch and its wooden module

Fig. 17

Side elevations of the formwork; a marking the base which is a inverted Takagi–Landsberg curve, b making the steel frame as a supporting base; c placing the wooden modules (trussed arches) on the vertices of the base and connected the modules with flat wooden panels for laying reinforced concrete

Fig. 18

An impression of the fractal-based hypar structure having w = 0.75, and height = 9.72 m

Conclusion

This paper has used fractal geometry to develop a parametric model of a hypar that can be transformed from its smooth profile to an unsmooth fractal-based profile using IFS-based Midpoint Displacement Method. This method has produced a range of different hypar shapes having different levels of surface irregularities ranging from smooth to unsmooth out of which some aesthetically original and structurally optimal forms have been found based on different supporting and boundary conditions. The structural analyses have shown that the smooth hypar is stronger for the supporting system 1, while the fractal-based irregular hypar is stronger for the supporting system 2 by considering the maximum nodal displacement as a factor of measuring the structural optimality and global stiffness. It is important to mention that the maximum displacements are only observed at the corners of all the variations of the parametric hypar under the supporting system 2. This indicates that the relative optimal performance of smooth and irregular hypars, in terms of their deflections, are affected by the corner segments which are, structurally speaking, largely unnecessary. However, keeping the architectural preference of the maximum covered area with the minimum supports, the corners and their deflections have been accounted for when finding the optimality. Nevertheless, the maximum nodal deflections do not guarantee the optimal shape of a structure because other factors, such as the buckling, bending, cracking and stability, are equally important to determine the actual strength of a structure. Apart from the structural factors, the optimization process has not considered other important parameters such as the cost of construction, or functionality. In a future study, other factors including comprehensive structural behavior can be further analyzed.