Abstract
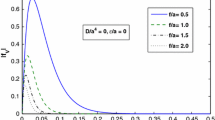
The problem of hydrodynamic loads due to the interaction of a gravity current propagating over a bottom channel with a submerged circular cylinder is studied experimentally. It was shown that in the examined range of parameters, the hydrodynamic loads are simulated after Froude. The hydrodynamic loads are maximal if the cylinder lies on the bottom, and they decrease rapidly with increase in the distance from the cylinder to the channel bottom. The effects of mixing and entrainment on the nature of the hydrodynamic loads are considered.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
REFERENCES
J. E. Simpson, Gravity Currents: In the Environment and Laboratory, Cambridge Univ. Press, Cambridge (1997).
V. Yu. Liapidevskii and V. M. Teshukov, “Mathematical models for the propagation of long waves in an inhomogeneous fluid,” Izd. Sib. Otd. Ross. Akad. Nauk, Novosibirsk (2000).
C. Hartel, E. Meiburg, and F. Meiburg, “Analysis and direct numerical simulation of the flow at a gravity-current head. 1. Flow topology and front velocity for slip and no-slip boundary,” J. Fluid Mech., 41, 189–212 (2000).
L. P. Thomas, S. B. Dalziel, and B. M. Marino, “The structure of the head of an inertial gravity current determined by particle-tracking velocimetry,” Exper. Fluids, 34, 708–716 (2003).
J. D. Parsons and M. H. Garcia, “Similarity of gravity flow fronts,” Phys. Fluids, 10, No. 12, 3209–3213 (1998).
J. W. Rottman, J. E. Simpson, J. S. R. Hunt, and R. E. Britter, “Unsteady gravity flows over obstacles,” J. Hazardous Mat., 11, 325–340 (1985).
G. F. Lane-Serff, L. M. Beal, and T. D. Hadfield, “Gravity flow over obstacles,” J. Fluid Mech., 292, 39–53 (1995).
N. V. Gavrilov and E. V. Ermanyuk, “Effect of a pycnolcine on forces exerted by internal waves on a stationary cylinder,” J. Appl. Mech. Tech. Fiz., 37, No. 6, 825–831 (1996).
V. I. Bukreev and N. V. Gavrilov, “Perturbations ahead of a wing moving in a stratified fluid,” J. Appl. Mech. Tech. Fiz., No. 2, 257–259 (1990).
T. B. Benjamin, “Gravity flows and related phenomena,” J. Fluid Mech., 31, pt 2, 209–248 (1968).
M. Moghisi and P. T. Squire, “An experimental investigation of the initial force of impact on a sphere striking a fluid surface,” J. Fluid Mech., 108, 133–146 (1981).
L. I. Sedov, Similarity and Dimension Methods in Mechanics [in Russian], Nauka, Moscow (1972).
V. I. Bukreev, A. V. Gusev, and E. M. Romanov, “Effect of molecular diffusion on the stability of stratified shear flows,” Izv. Ross. Akad. Nauk, Mekh. Zhidk. Gaza, No. 1, 35–40 (1993).
Author information
Authors and Affiliations
Additional information
Translated from Prikladnaya Mekhanika i Tekhnicheskaya Fizika, Vol. 46, No. 2, pp. 81–90, March–April, 2005.
Rights and permissions
About this article
Cite this article
Ermanyuk, E.V., Gavrilov, N.V. Interaction of an internal gravity current with a submerged circular cylinder. J Appl Mech Tech Phys 46, 216–223 (2005). https://doi.org/10.1007/PL00021899
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/PL00021899