Bifurcating fronts for the Taylor—Couette problem in infinite cylinders

Abstract.

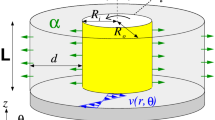
We show the existence of bifurcating fronts for the weakly unstable Taylor—Couette problem in an infinite cylinder. These fronts connect a stationary bifurcating pattern, here the Taylor vortices, with the trivial ground state, here the Couette flow. In order to show the existence result we improve a method which was already used in establishing the existence of bifurcating fronts for the Swift—Hohenberg equation by Collet and Eckmann, 1986, and by Eckmann and Wayne, 1991. The existence proof is based on spatial dynamics and center manifold theory. One of the difficulties in applying center manifold theory comes from an infinite number of eigenvalues on the imaginary axis for vanishing bifurcation parameter. But nevertheless, a finite dimensional reduction is possible, since the eigenvalues leave the imaginary axis with different velocities, if the bifurcation parameter is increased. In contrast to previous work we have to use normalform methods and a non–standard cut–off function to obtain a center manifold which is large enough to contain the bifurcating fronts.