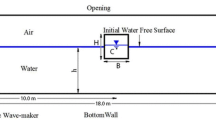
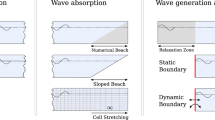
Abstract
A Volume of Fluid (VOF) technique has been further developed and coupled with an incompressible Euler/Navier Stokes solver operating on adaptive, unstructured grids to simulate the interactions of extreme waves and a LNG carrier with full or partially filled tanks. The present implementation follows the classic VOF implementation for the liquid-gas system, considering only the liquid phase. Extrapolation algorithms are used to obtain velocities and pressures in the gas region near the free surface. An arbitrary Lagrangian-Eulerian (ALE) frame of reference is used. The mesh is moved in such a way as to minimize the distortion of the mesh due to body movement. The incompressible Euler/Navier-Stokes equations are solved using projection schemes and a finite element method on unstructured grids, and the free surface is captured by the VOF method. The computer code developed based on the method described above is used in this study to simulate a numerical seakeeping tank, where the waves are generated by the sinusoidal excitation of a piston paddle, and a freely-floating LNG carrier with full or partially filled tanks moves in response to the waves. Both head sea and oblique sea are considered in the simulation. Highly nonlinear wave-body interactions, such as green water on deck and sloshing, have been modeled successfully.
Similar content being viewed by others
References
Nichols, B.D. and Hirt, C.W. Methods for Calculating Multi-Dimensional, Transient Free Surface Flows Past Bodies, Proc. First Intern. Conf. Num. Ship Hydrodynamics, Research Gaithersburg, ML, Oct. 20–23 (1975).
Hirt, C.W. and Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries, Journal of Computational Physics 39, 201 (1981).
Scardovelli, R.; Zaleski, S. Direct numerical simulation of free-surface and interfacial Flow, Annual Review of Fluid Mechanics 31: 567–603 (1999).
Chen, G., Kharif, C. Two-Dimensional Navier-Stokes Simulation of Breaking Waves, Physics of Fluids, 11(1), 121–133, (1999).
Biausser, B., Fraunie, P., Grilli, S. and Marcer R. Numerical analysis of the internal kinematics and dynamics of three dimensional breaking waves on slopes, International Journal of Offshore and Polar Engineering, Vol. 14, No. 4 (2004).
Fekken, G., Veldman, A.E.P. and Buchner, B. Simulation of Green Water Loading Using the Navier-Stokes Equations, Proc. of the 7th Int. Conf. on Numerical Ship Hydrodynamics, Nantes, France (1999).
Huijsmans, R.H.M. and van Grosen, E. Coupling Freak Wave Effects with Green Water Simulations, Proceeding of the 14th ISOPE, Toulon, France, May 23–28 (2004).
Rhee, S.H. Unstructured Grid Based Reynolds-Averaged Navier-Stokes Method for Liquid Tank Sloshing, Journal of Fluids Engineering, Volume 127, Issue 3, pp. 572–582 (2005).
Yang, C. and Löhner, R. Computation of 3D Flows with Violent Free Surface Motion, Proceeding of the 15th ISOPE, Seoul, Korea, June 19–24 (2005).
Löhner, R. A Fast Finite Element Solver for Incompressible Flows, AIAA-90-0398 (1990).
Löhner, R. A Fast Finite Element Solver for Incompressible Flows, AIAA-90-0398 (1993).
Yang, C. and Löhner, R. Fully Nonlinear Ship Wave Calculation Using Unstructured Grids and Parallel Computing, Proc. 3rd Osaka Col. on Advanced CFD Appl. to Ship Flow and Hull Form Design, Osaka, Japan (1998).
Löhner, R., Yang, C., Onate, E. and Idelssohn, S. An Unstructured Grid-Based, Parallel Free Surface Solver, Appl. Num. Math. 31, 271–293 (1999).
Löhner, R. Applied CFD Techniques; J. Wiley & Sons (2001).
Löhner, R. Multistage Explicit Advective Prediction for Projection-Type Incompressible Flow Solvers, J. Comp. Phys. 195, 143–152 (2004).
Löhner, R., Yang, C., Cebral, J., Camelli, F., Soto, O. and Waltz, J. Improving the Speed and Accuracy of Projection-Type Incompressible Flow Solvers, Computer Methods in Applied Mechanics and Engineering, Vol. 195, Issues 23–24, April 2006, pp. 3087–3109.
Martin, J.C. and Moyce, W.J. An Experimental Study of the Collapse of a Liquid Column on a Rigid Horizontal Plane, Phil. Trans. Royal Soc. London A244, 312–324 (1952).
Hansbo, P. The Characteristic Streamline Diffusion Method for the Time-Dependent Incompressible Navier-Stokes Equations, Comp. Meth. Appl. Mech. Eng. 99, 171–186 (1992).
Köolke, A. Modellierung und Diskretisierung bewegter Diskontinuit’aten in Randgekoppelten Mehrfeldaufgaben, Ph.D. Thesis, TU Braunschweig (2005).
Landrini, M., Colagorossi, A. and Faltisen, O.M. Sloshing in 2-D Flows by the SPH Method, Proc. of the 8th Int. Conf. on Num. Ship Hydro., Busan, Korea (2003).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Yang, C., Löhner, R. & Lu, H. An unstructured-grid based volume-of-fluid method for extreme wave and freely-floating structure interactions. J Hydrodyn 18 (Suppl 1), 405–412 (2006). https://doi.org/10.1007/BF03400480
Published:
Issue Date:
DOI: https://doi.org/10.1007/BF03400480