Abstract
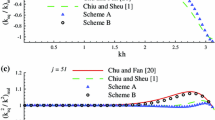
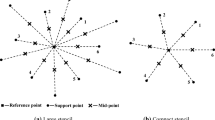
A three-point explicit compact difference scheme with high order of accuracy for solving the unsteady incompressible Navier-Stokes equations was presented. Numerical solutions are obtained for the model problem of lid-driven cavity flow and are compared with benchmark solutions found in the literature. It is discovered that the proposed three point explicit compact scheme is not only simple to implement and economical to use, but also is effective to obtain high-order accurate solution in coarse grid systems.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Ghia U., Ghia K.N., Shin C.T. High-Re solutions for imcompressible flow using the Navier-Stokes equation and a multigrid method [J]. Journal of Computational Physics, 1982, 48(3): 387–411.
Barragy E., Carey G.F. Stream function-vorticity driven cavity solutions using p finite elements [J]. Computers and Fluids, 1997; 26:453–468.
Liao S. J. Higher-order streamfunction-vorticity formulation of 2-D steady state Navier–Stokes equations [J]. International Journal for Numerical Methods in Fluids, 1992; 15:595–612.
Kim J., Moin P. Application of a fractional-step method to incompressible navier-stokes equations [J]. Journal of Computational Physics, 1985, 59: 308–323.
Botella O., Peyret R. Benchmark spectral results on the lid-driven cavity flow [J]. Computers and Fluids, 1998; 27:421–433.
Gupta M.M. High accuracy solutions of incompressible Navier–Stokes equations [J]. Journal of Computational Physics, 1991; 93:343–359.
Li M, Tang T, Fornberg B. A compact fourth-order finite difference scheme for the steady incompressible Navier–Stokes equations [J]. International Journal for Numerical Methods in Fluids, 1995; 20:1137–1151.
Shankar P.N., Deshpande M.D. Fluid mechanics in the driven cavity [J]. Annual Review of Fluid Mechanics, 2000; 32:93–136.
Erturk, E.; Corke, T.C.; Gokcol, C. Numerical solutions of 2-D steady incompressible driven cavity flow at high Reynolds numbers [J]. International Journal for Numerical Methods in Fluids, 2005; 48:747–774.
Sousa E., Sobey I.J. Effect of boundary vorticity discretization on explicit stream-function vorticity calculations [J]. International Journal for Numerical Methods in Fluids, 2005; 49:371–393.
Briley W.R. A numerical study of laminar separation bubbles using the Navier-Stokes equations [J]. Journal of Fluid Mechanics, 1971, 47: 713–736.
Author information
Authors and Affiliations
Corresponding author
Additional information
Project supported by the National Natural Science Foundation of China (Grant No: 50479053).
Biography: LIN Jian-guo (1960-), Male, Ph.D., Professor
Rights and permissions
About this article
Cite this article
Lin, Jg., Xie, Zh. & Zhou, Jt. Application of a three-point explicit compact difference scheme to the incompressible Navier-Stokes equations. J Hydrodyn 18 (Suppl 1), 151–156 (2006). https://doi.org/10.1007/BF03400439
Published:
Issue Date:
DOI: https://doi.org/10.1007/BF03400439