Skip to main content
SpringerLink
Log in

Simulations of interactions between nonlinear waves and multi or an array of cylinders

  • Session B2
  • Published:
Journal of Hydrodynamics Aims and scope Submit manuscript

Abstract

Computational methods are developed to simulate interactions of nonlinear waves with multi-structures through the finite element method based on second order and fully nonlinear theories. The three dimensional (3D) mesh with prism elements is generated through an extension of a two dimensional (2D) unstructured grid. The potential and velocity in the fluid field are obtained by solving finite element matrix equations at each time step using the conjugate gradient method with SSOR preconditioner. The combined Sommerfeld-Orlanski radiation condition and the damping zone method is used to minimize wave reflection. The regridding and smoothing techniques are employed to improve the stability of the solution and the accuracy of the result.

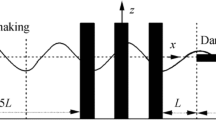
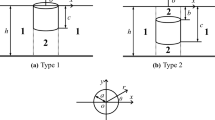
The method is first used to simulate interactions of waves and an array of cylinders in the time domain based on the second order theory. Numerical simulations show that the influence of mutual interference between cylinders is highly significant. In particular, the first order and the second order results can become quite large when their corresponding wave number is close to the trapped mode. Simulations based on the fully nonlinear theory are also made for the 3D interactions between fixed multi-cylinders and waves generated by a piston type wave maker in a numerical tank with an artificial beach. Extensive results of practical importance have been obtained, which have been overlooked in many previous applications. The developed method is further employed to solve the 3D fully nonlinear radiation problems by multi-cylinders undergoing large amplitude oscillations in the open sea. All these different applications have clearly demonstrated the flexibility of the method. The simulations also show that the developed method is highly efficient and has great potential to be used for large scale calculation in the motions of floating structures in nonlinear waves.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Abul-Azm, A.G. and Williams, A.N. Second order diffraction loads on truncated cylinders, J. Waterway, Port, Coastal and Ocean Eng., ASCE, 1988, 114, 436–454.

    Article  Google Scholar 

  2. Eatock Taylor, R., Hung, S.M. Wave drift enhancement effects in multi column structures, Appl. Ocean Res., 1985, 7, 128–137.

    Article  Google Scholar 

  3. Eatock Taylor R., Hung, S.M. Second order diffraction force on a vertical cylinder in regular waves, Appl. Ocean Res., 1987, 9, 19–31.

    Article  Google Scholar 

  4. Chau, F.P. The second order velocity potential for diffraction of waves by fixed offshore structures, PhD thesis, University of London, 1989.

  5. Evans, D.V. and Porter, R. Trapped modes about multiple cylinders in a channel, J. Fluid Mech., 1997, 339, 331–356.

    Article  MathSciNet  Google Scholar 

  6. Hecht F. BAMG: Bidimensional anisotropic mesh generator, website: http://www-rocq1.inria.fr/gamma/cdrom/www/bamg/eng.htm, 1998.

  7. Hu, P.X., Wu G.X. and Ma Q.W. Numerical simulation of nonlinear wave radiation by a moving vertical cylinder, Ocean Engng, 2002, 29, 1733–1750.

    Article  Google Scholar 

  8. Isaacson, M. and Cheung, K.F. Time-domain solution for second-order wave diffraction, J. Waterway, Port, Coastal and Ocean Eng., ASCE, 1990, 116, 191–210.

    Article  Google Scholar 

  9. Isaacson, M. and Cheung, K.F. Second order wave diffraction around two-dimensional bodies by time-domain method, Appl. Ocean Res., 1991, 13(4), 175–186.

    Article  Google Scholar 

  10. Isaacson, M. and Cheung, K.F. Time-domain second-order wave diffraction in three dimensions, J. Waterway, Port, Coastal and Ocean Eng., ASCE, 1992, 118, 496–516.

    Article  Google Scholar 

  11. Kashiwagi, M. and Ohwatari, Y. First- and Second-Order Water Waves Around an Array of Floating Vertical Cylinders, Proc. 17 th Workshop on water waves and Floating Bodies, 2002, Cambridge, UK.

  12. Kim, M.H. and Yue, D.K.P. The complete second-order diffraction solution for anaxisymmetric body. Part II. Bichromatic incident waves, J. Fluid Mech., 1989, 200, 235–264.

    Article  MathSciNet  Google Scholar 

  13. Lighthill, M. J. Waves and hydrodynamic loading, Proc. 2 nd Int. BOSS Conf., 1979, London, 1–40.

  14. Linton, C.M. and Evans, D.V. The interaction of waves with arrays of vertical circular cylinders, J. Fluid Mech., 1990, 215, 549–569.

    Article  MathSciNet  Google Scholar 

  15. Ma, Q.W., Wu, G.X. and Eatock Taylor, R. Finite element simulation of fully nonlinear interaction between vertical cylinders and steep waves. Part 1: Methodology and numerical procedure, Int. J. for Num. Methods in Fluids, 2001a, 36, 265–285.

    Article  Google Scholar 

  16. Ma, Q.W., Wu, G.X. and Eatock Taylor, R. Finite element simulation of fully nonlinear interaction between vertical cylinders and steep waves. Part 2: Numerical results and validation, Int. J. for Num. Methods in Fluids, 2001a, 36, 287–308.

    Article  Google Scholar 

  17. Malenica, S., Eatock Taylor, R. and Huang, J.B. Second order water wave diffraction by an array of vertical cylinders, J. Fluid Mech., 1999, 390, 349–373.

    Article  MathSciNet  Google Scholar 

  18. Maniar, H.D. and Newman, J.N. Wave diffraction by a long array of cylinders, J. Fluid Mech., 1997, 339, 309–330.

    Article  MathSciNet  Google Scholar 

  19. Mavrakos, S.A. and Koumoutsakos, P. Hydrodynamic interaction among vertical axisymmetric bodies restrained in waves, Appl. Ocean Res., 1987, 9, 128–140.

    Article  Google Scholar 

  20. Molin, B. Second order diffraction loads upon three-dimension bodies, Appl. Ocean Res., 1979, 1, 197–202.

    Article  Google Scholar 

  21. Molin, B. and Marion, A. Second order loads and motions for floating bodies in regular waves, Proc. Offshore Mechanics and Artic Engineering, 1986, Tokyo, 353-360.

  22. Ohl, C.O.G, Eatock Taylor, R. Taylor, P. H. and Borthwick A.G.L. Water wave diffraction by a cylinder array. Part 1. Regular waves, J. Fluid. Mech., 2001, 442, 1–32.

    MATH  Google Scholar 

  23. Rahman, M, and Satish, M.G. First-order diffraction forces on a pair of cylinders, Ocean Engng, 1991, 18, 101–110.

    Article  Google Scholar 

  24. Vada, T. A numerical solution of second-order wave-diffraction problem for submerged cylinder of arbitrary shape, J. Fluid. Mech., 1987, 174, 23–37.

    Article  Google Scholar 

  25. Wu, G.X. On the second order wave reflection and transmission by a horizontal cylinder, Appl. Ocean Res., 1991, 13, 58–62.

    Article  Google Scholar 

  26. Wu, G.X. and Eatcok Taylor, R. Second order diffraction forces on horizontal cylinders, J. of Hydrodynamics, 1989, 12, 55–65.

    MATH  Google Scholar 

  27. Wu, G.X. and Eatock Taylor R. The second order diffraction forces on horizontal cylinders in finite water depth, Appl. Ocean Res., 1990, 12, 106–111.

    Article  Google Scholar 

  28. Wu, G.X. and Eatock Taylor, R. Transient motion of a floating body in steep water waves, Proc. 11 th Workshop on water waves and Floating Bodies, 1996, Hamburg.

  29. Wu, G.X. and Eatock Taylor, R. The coupled finite element and boundary element analysis of nonlinear interactions between waves and bodies, Ocean Engng, 2003, 30, 387–400

    Article  Google Scholar 

  30. Wu, G.X. and Hu, Z.Z. Simulation of Nonlinear Interactions between Waves and Floating Bodies through a Finite Element Based Numerical Tank, Proc. R. Soc. Lond. A, 2004, 460, 2797–2817.

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, University College London, Torrington Place, London, WC1E 7JE, UK

    C. Z. Wang &  G. X. Wu

  2. Long Jiang Professor, College of Shipbuilding Engineering, Harbin Engineering University, Harbin, 150001, China

    G. X. Wu

Authors
  1. C. Z. Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. G. X. Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wang, C.Z., Wu, G.X. Simulations of interactions between nonlinear waves and multi or an array of cylinders. J Hydrodyn 18 (Suppl 1), 125–132 (2006). https://doi.org/10.1007/BF03400435

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF03400435

Key words

Search

Navigation