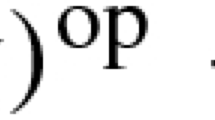Abstract
Let \({\cal P}\) be the point set of an absolute plane, let \({\cal {\tilde P}}\) be the set of all point reflections, let ℳ, resp. ℳ+, be the group of all, resp. of all proper, motions and let
be the map where \({\widetilde {a,\ b}}\) denotes the uniquely determined point-reflection interchanging a and b.
Then
is called the defect function, or shortly the defect.
We show that δa;b,c is a rotation around the point a where the angle of δa;b,c is exactly the angle defect of the triangle (a, b, c) (cfr. 3.5).
After fixing a point \(o\ \in {\cal P}\) and setting \(a+b\:=\widetilde {o,\ a}\ {\rm o}\ {\tilde o}\ (b),\ ({\cal P},+)\) becomes a K-loop and the so called precession function
of the loop (\({\cal P}, +)\) coincides with the defect of the triangle (o, a, −b) (cfr. (4.4.1)), hence δa,b = δo;a,−b for all \(a, b \in {\cal P}\).
With the order relation of the absolute plane we associate an orientation function
defined on the pairs of triangles (cfr. (2.8)). If (a, b, c) ∈ Δ is a triangle and d a point of the line \(\overline {b,\ c}\) 1, then (cfr. (3.9.2)):
and moreover, if d is even a point of the open segment ]b, c[ then (cfr. (2.8.5)):
Thus the angle defect of the triangle (a, b, c) is the sum of the angle defects of the triangles (a, b, d) and (a, d, c).
Similar content being viewed by others
References
H. Karzel. Recent developments on absolute geometries and algebraization by K-loops. Discrete Math. 208/209 (1999), 387–409.
H. Karzel, H.-J. Kroll. Geschichte der Geometrie seit Hilbert, Wissenschaftliche Buchgesellschaft, Darmstadt, 1988.
H.Karzel, M.Marchi. Introduction of Measures for Segments and Angles in a general Absolute Plane, Discrete Math. (submitted).
H.Karzel, M.Marchi. Classification of general absolute geometries with Lambert-Saccheri quadrangles, (to appear).
H.Karzel, M.Marchi. The defect in an invariant Reflection Structure (to appear).
H. Karzel, K. SÖrensen, D. Windelberg. Einführung in die Geometrie, Vandenhoeck, Göttingen, 1973.
H. Karzel, H. Wefelscheid. A geometric construction of the K-loop of a hyperbolic space, Geom. Dedicata 58 (1995) 227–236.
H. Kiechle. Theory of K-loops, Lecture Notes in Mathematics, Springer-Verlag, Berlin, 2002.
Author information
Authors and Affiliations
Additional information
This work was partially supported by the research project of MIUR (Italian Ministry of Education, University and Research) “Strutture geometriche, combinatoria e loro applicazioni” and by the research group GNSAGA of INDAM
Rights and permissions
About this article
Cite this article
Karzel, H., Marchi, M. Relations between the K-loop and the defect of an absolute plane. Results. Math. 47, 305–326 (2005). https://doi.org/10.1007/BF03323031
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/BF03323031