Abstract
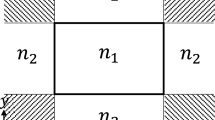
Diffraction of a plane electromagnetic wave (E-polarization) by two orthogonal electrically resistive half-planes is analyzed. The physical problem reduces to a Riemann-Hilbert problem in the real axis for four pairs of analytic functions \(\Phi^+_j(\eta)(\eta\ \in\ \rm C^+)$$ and $$\Phi^-_j(\eta) = \Phi^+_j (-\eta)(\eta\ \in\ {\rm C}^-),j = 1,2,3,4,\) where ℂ+ and ℂ are the upper and lower half-planes. It is shown that the problem is equivalent to two scalar Riemann-Hilbert problems on a plane and a Riemann-Hilbert problem on a genus-3 hyperelliptic surface subject to a certain symmetry condition. A closed-form solution is derived in terms of singular integrals and the genus-3 Riemann Theta function.
Similar content being viewed by others
References
Y. A. Antipov, A symmetric Riemann-Hilbert problem for order-4 vectors in diffraction theory, Quart. J. Mech. Appl. Math. 63 (2010), 349–374.
Y. A. Antipov and N. G. Moiseev, Exact solution of the plane problem for a composite plane with a cut across the boundary between two media, J. Appl. Math. Mech. (PMM) 55 (1991), 531–539.
Y. A. Antipov and V. V. Silvestrov, Factorization on a Riemann surface in scattering theory, Quart. J. Mech. Appl. Math. 55 (2002), 607–654.
Y. A. Antipov and V. V. Silvestrov, Second-order functional-difference equations. I.: Method of the Riemann-Hilbert problem on Riemann surfaces, Quart. J. Mech. Appl. Math. 57 (2004), 245–265.
Y. A. Antipov and V. V. Silvestrov, Second-order functional-difference equations. II.: Scattering from a right-angled conductive wedge for E-polarization, Quart. J. Mech. Appl. Math. 57 (2004), 267–313.
Y. A. Antipov and V. V. Silvestrov, Vector functional-difference equation in electromagnetic scattering, IMA J. Appl. Math. 69 (2004), 27–69.
Y. A. Antipov and V. V. Silvestrov, Electromagnetic scattering from an anisotropic half-plane at oblique incidence: the exact solution, Quart. J. Mech. Appl. Math. 59 (2006), 211–251.
Y. A. Antipov and V. V. Silvestrov, Method of Riemann surfaces in the study of supercavitating flow around two hydrofoils in a channel, Physica D 235 (2007), 72–81.
Y. A. Antipov and A. Y. Zemlyanova, Motion of a yawed supercavitating wedge beneath a free surface, SIAM J. Appl. Math. 70 (2009), 923–948.
E. D. Belokolos, A. I. Bobenko, V. Z. Enol’skii, A. R. Its and V. B. Matveev, Algebro-Geometric Approach to Nonlinear Integrable Equations, Springer-Verlag, Berlin etc., 1994.
G. P. Cherepanov, Solution of a linear boundary value problem of Riemann for two functions and its application to certain mixed problems in the plane theory of elasticity, J. Appl. Math. Mech. (PMM) 26 (1962), 1369–1377.
V. G. Daniele, The Wiener-Hopf technique for impenetrable wedges having arbitrary aperture angle, SIAM J. Appl. Math. 63 (2003), 1442–1460.
A. Krazer, Lehrbuch der Thetafunktionen, Teubner, Leipzig, 1903.
S. R. Legault and T. B. A. Senior, Solution of a second-order difference equation using the bilinear relations of Riemann, J. Math. Phys. 43 (2002), 1598–1621.
N. G. Moiseev, Factorization of matrix functions of special form, Sov. Math. Dokl. 39 (1989), 264–267.
N. G. Moiseev and G. Ya. Popov, Exact solution of the problem of bending of a semiinfinite plate completely bonded to an elastic half-space, Izv. AN SSSR, Solid Mechanics 25 (1990), 113–125.
B. M. Nuller, Contact problems for a system of a elastic half-planes, J. Appl. Math. Mech.(PMM) 54 (1990), 249–253.
V. V. Silvestrov, On the elastic stress and strain state near a spatial crack on a two-sheeted surface, J. Appl. Math. Mech. (PMM) 54 (1990), 99–106.
V. V. Silvestrov, The method of Riemann surfaces in the problem of interface cracks and inclusions under concentrated forces, Iz. VUZ 48 (2005), 75–88.
E. I. Zverovich, Boundary value problems in the theory of analytic functions in Hölder classes on Riemann surfaces, Russian Math. Surveys 26 (1971),117–192.
E. I. Zverovich, A mixed problem of elasticity theory for the plane with cuts that lie on the real axis. Proc. Symp. Continuum Mechanics and Related Problems of Analysis (Tbilisi, 1971), Vol. 1, 103–114, Mecniereba, Tbilisi, 1973,
Author information
Authors and Affiliations
Corresponding author
Additional information
Work partly funded by National Science Foundation through grant DMS0707724
Rights and permissions
About this article
Cite this article
Antipov, Y.A. A Genus-3 Riemann-Hilbert Problem and Diffraction of a Wave by Two Orthogonal Resistive Half-Planes. Comput. Methods Funct. Theory 11, 439–462 (2012). https://doi.org/10.1007/BF03321871
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/BF03321871