Motion and deformation of viscous drop in stokes flow near rigid wall

Abstract

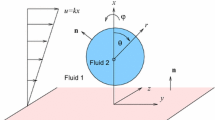
A boundary integral method was developed for simulating the motion and deformation of a viscous drop in an axisymmetric ambient Stokes flow near a rigid wall and for direct calculating the stress on the wall. Numerical experiments by the method were performed for different initial stand-off distances of the drop to the wall, viscosity ratios, combined surface tension and buoyancy parameters and ambient flow parameters. Numerical results show that due to the action of ambient flow and buoyancy the drop is compressed and stretched respectively in axial and radial directions when time goes. When the ambient flow action is weaker than that of the buoyancy the drop raises and bends upward and the stress on the wall induced by drop motion decreases when time advances. When the ambient flow action is stronger than that of the buoyancy the drop descends and becomes flatter and flatter as time goes. In this case when the initial stand-off distance is large the stress on the wall increases as the drop evolutes but when the stand-off distance is small the stress on the wall decreases as a result of combined effects of ambient flow, buoyancy and the stronger wall action to the flow. The action of the stress on the wall induced by drop motion is restricted in an area near the symmetric axis, which increases when the initial stand-off distance increases. When the initial stand-off distance increases the stress induced by drop motion decreases substantially. The surface tension effects resist the deformation and smooth the profile of the drop surfaces. The drop viscosity will reduce the deformation and migration of the drop.