Skip to main content
SpringerLink
Log in

Tumbling dynamics of rod-like and semi-flexible polymers in simple shear and mixed flows

  • Published:
Macromolecular Research Aims and scope Submit manuscript

Abstract

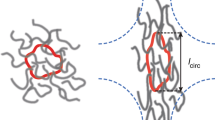
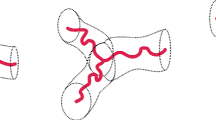
In this work, we focus on the tumbling dynamics of rod-like and semi-flexible polymers in mixed flows, which vary from simple shear to pure rotation. By employing a bead-rod model, the tumbling pathways and periods are examined with a focus on the angular distribution of their orientation. Under the mixed flows, the tumbling dynamics agreed well with earlier studies and confirmed the predicted scaling laws. We found that the angular distribution deviates from that of shear flow as the flow type approaches pure rotation. Finally, we investigated the angular distribution of λ-DNA in a shear flow and found that the present numerical simulations were in quantitative agreement with the previous experimental data.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. P. S. Doyle, J. Bibette, A. Bancaud, and J. L. Viovy,Science,295, 2237 (2002).

    Article  CAS  Google Scholar 

  2. N. P. Teclemariam, V. A. Beck, E. S. G. Shaqfeh, and S. J. Muller,Macromol.,40, 3848 (2007).

    Article  CAS  Google Scholar 

  3. J. M. Kim and P. S. Doyle,Lab Chip,7, 213 (2007).

    Article  CAS  Google Scholar 

  4. R. G. Larson,J. Rheol.,49, 1 (2005).

    Article  CAS  Google Scholar 

  5. E. S. G. Shaqfeh,J. Non-Newton. Fluid Mech.,130, 1 (2005).

    Article  CAS  Google Scholar 

  6. T. T. Perkins, D. E. Smith, and S. Chu,Science,276, 2016 (1997).

    Article  CAS  Google Scholar 

  7. D. E. Smith, H. P. Babcock, and S. Chu,Science,283, 1724 (1999).

    Article  CAS  Google Scholar 

  8. C. M. Schroeder, R. E. Teixeira, E. S. G. Shaqfeh, and S. Chu,Phys. Rev. Lett.,95, 018301 (2005).

    Article  Google Scholar 

  9. R. E. Teixeira, H. P. Babcock, E. S. G. Shaqfeh, and S. Chu,Macromolecules,38, 581 (2005).

    Article  CAS  Google Scholar 

  10. J. S. Lee, R. Dylla-Spears, N. P. Teclemariam, and S. J. Muller,Appl. Phys. Lett.,90, 074103 (2007).

    Article  Google Scholar 

  11. A. Celani, A. Puliafito, and K. Turitsyn,Europhys. Lett.,70, 464 (2005).

    Article  CAS  Google Scholar 

  12. K. S. Turitsyn,J. Exp. Theo. Phys.,105, 655 (2007).

    Article  CAS  Google Scholar 

  13. S. Gerashchenko and V. Steinberg,Phys. Rev. Lett.,96, 038304 (2006).

    Article  Google Scholar 

  14. J. S. Lee, E. S. G. Shaqfeh, and S. J. Muller,Phys. Rev. E,75, 040802 (2007).

    Article  Google Scholar 

  15. B. Maier and J. O. Radler,Macromolecules,33, 7185 (2000).

    Article  CAS  Google Scholar 

  16. R. B. Bird, C. F. Curtiss, R. C. Armstrong, and O. Hassager,Dynamics of Polymeric Liquids, Wiley, New York, 1987, Vol. 2.

    Google Scholar 

  17. P. S. Doyle, E. S. G. Shaqfeh, and A. P. Gast,J. Fluid Mech.,334, 251 (1997).

    Article  CAS  Google Scholar 

  18. M. Doi and S. F. Edwards,The Theory of Polymer Dynamics, Oxford Univ. Press, 1988.

  19. A. Puliafito and K. Turitsyn,Physica D,211, 9 (2005).

    Article  CAS  Google Scholar 

  20. E. J. Hinch and L. G. Leal,J. Fluid Mech.,92, 591 (1979).

    Article  Google Scholar 

  21. M. Somasi, B. Khomami, N. J. Woo, J. S. Hur, and E. S. G. Shaqfeh, J. Non-Newton.Fluid Mech.,108, 227 (2002).

    CAS  Google Scholar 

  22. T. W. Liu,J. Chem. Phys.,90, 5826 (1989).

    Article  CAS  Google Scholar 

  23. C. C. Hsieh, S. Jain, and R. G. Larson,J. Chem. Phys.,124, 044911 (2006).

    Article  Google Scholar 

  24. J. S. Hur, E. S. G. Shaqfeh, and R. G. Larson,J. Rheol.,44, 713 (2000).

    Article  CAS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Battery R&D, LG Chem / Research Park, 305-380, Daejeon, Korea

    Joo Sung Lee

  2. Department of Chemical Engineering, Ajou University, 443-749, Suwon, Korea

    Ju Min Kim

Authors
  1. Joo Sung Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ju Min Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ju Min Kim.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Lee, J.S., Kim, J.M. Tumbling dynamics of rod-like and semi-flexible polymers in simple shear and mixed flows. Macromol. Res. 17, 807–812 (2009). https://doi.org/10.1007/BF03218618

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF03218618

Keywords

Search

Navigation