Skip to main content
SpringerLink
Log in

The onset of natural convection and heat transfer correlation in horizontal fluid layer heated uniformly from below

  • Thermal Engineering · Fluid Engineering · Energy and Power Engineering
  • Published:
KSME International Journal Aims and scope Submit manuscript

Abstract

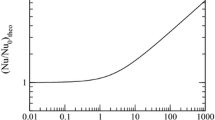
The critical condition of the onset of buoyancy-driven convective motion of uniformly heated horizontal fluid layer was analysed by the propagation theory which transforms the disturbance quantities similarly. The dimensionless critical time,τ c , is obtained as a function of the Rayleigh number and the Prandtl number. Based on the stability criteria and the boundary-layer instability model, a new heat transfer correlation which can cover whole range of Rayleigh number was derived. Our theoretical results predict the experimental results quite reasonably.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

a:

Horizontal wave number [−]

d:

Fluid depth [m]

g:

Gravitational acceleration [m/s2]

k:

Thermal conductivity [J/mK]

Nu:

Nusselt number (=qw/kΔT) [−]

P:

Pressure [Pa]

Pr:

Prandtl number (=ν/α) [−]

Ra:

Rayleigh number (=gβΔTd3/αν) [−]

Raq :

Rayleigh number based on the heat flux (=gβqwd4/kαν) [−]

qw :

Wall heat flux [J/m2]

T:

Temperature [K]

t:

Time [s]

\(\overrightarrow U \) :

Velocity vector [m/s]

w:

Dimensionless vertical velocity [−]

X, Y, Z:

Space in Cartesian coordinate [m]

α:

Thermal diffusivity [m2/s]

β:

Thermal expansion coefficient [1/K]

ΔT:

Temperature difference [K]

ζ:

Similarity variable [−]

θ:

Dimensionless temperature [−]

μ:

Viscosity [Pa s]

ν:

Kinematic viscosity [m2/s]

ρ:

Density [kg/m3]

τ:

Dimensionless time [−]

0:

Basic quantity

1:

Disturbed quantity

References

  • Arpaci, V. S., 1997, “Microscales of Turbulent Heat and Mass Transfer Correlations,”Advances in Heat Transfer, Vol. 30, pp. 1–91.

    Google Scholar 

  • Busse, F. B., 1967, “On the Stability of Two-Dimensional Convection in a Layer Heated from Below,”J. Math. Phys., Vol. 46, pp. 140–150.

    MATH  Google Scholar 

  • Carslaw, H. S. and Jaeger, J. C., 1959,Conduction of Heat in Solid, 2nd ed., Oxford.

  • Chen, K. Chen, M. M. and Sohn, C. W., 1983, “Thermal Instability of Two-Dimensional Stagnation-Point Boundary Layers,”J. Fluid Mech., Vol. 132, pp. 49–63.

    Article  MATH  Google Scholar 

  • Cheung, F. B., 1980, “Heat Source-Driven Thermal Convection at Arbitrary Prandtl Number,”J. Fluid Mech., Vol. 97, pp. 734–758.

    Article  MathSciNet  Google Scholar 

  • Choi, C. K. and Kim, M. C., 1994, “Buoyancy Effects in Plane Couette Flow Heated from Below,”Proc. 10th Int. Heat Transfer Conf., Brighton, Vol. 5, pp. 453–458.

    Google Scholar 

  • Choi, C. K., Shin, C. B. and Hwang, S. T., 1986, “Thermal Instability in Thermal Entrance Region of Couette Flow Heated Uniformly from Below,”Proc. 8th Int. Heat Transfer Conf., San Francisco, Vol. 3, pp. 1389–1394.

    Google Scholar 

  • Chu, T. Y., 1990, “Developing Convection above a Finite Horizontal Surface,”Proc. 9th Int. Heat Transfer Conf., Jerusalem, Vol. 2, pp. 169–174.

    Google Scholar 

  • Chun, Y. H. and Choi, C. K., 1991, “Thermal Instability of Natural Convection over Inclined Isothermal Heated Plates,”Hwahak Konghak, Vol. 29, pp. 381–387 (in Korean).

    Google Scholar 

  • Currie, I. G., 1967, “The Effect of Heating Rate on the Stability of Stationary Fluid,”J. Fluid Mech., Vol. 29, pp. 337–347.

    Article  Google Scholar 

  • Foster, T. D., 1965, “Stability of Homogeneous Fluid Cooled Uniformly from Above,”Phys. Fluids, Vol. 8, pp. 1249–1257.

    Article  MathSciNet  Google Scholar 

  • Foster, T. D., 1969, “Onset of Manifest Convection in a Layer of Fluid with a Time-Dependent Surface Temperature,”Phys. Fluids, Vol. 12, pp. 2482–2487.

    Article  Google Scholar 

  • Howard, L. N., 1964, “Convection at High Rayleigh Numbers,”Proc. 11th Int. Cong. Appl. Mech., Munich, pp. 1109–1115.

  • Jhaveri, B. S. and Homsy, G. M., 1982, “The Onset of Convection in Fluid Layer Heated Rapidly in a Time-Dependent Manner,”J. Fluid Mech., Vol. 114, pp. 251–260.

    Article  MATH  Google Scholar 

  • Kim, M. C., Baik, J. S., Hwang, I. G., Yoon, D. Y., Choi, C. K., 1999a, “Buoyancy-Driven Convection in Plane Poiseuille Flow,”Chem. Eng. Sci., Vol. 54, pp. 619–632.

    Article  Google Scholar 

  • Kim, M. C., Choi, K. H. and Choi, C. K., 1999b, “The Onset of Thermal Convection in Initially, Stably Stratified Fluid Layer,”Int. J. Heat Mass Transfer, Vol. 42, pp. 4253–4258.

    Article  MATH  Google Scholar 

  • Kim, K.-H. and Kim, M.-U., 1986, “The Onset of Natural Convection in a Fluid Layer Suddenly Heated from Below,”Int. J. Heat Mass Transfer, Vol. 29, pp. 193–201.

    Article  MATH  Google Scholar 

  • Lick, W., 1965, “The Instability of a Fluid Layer with Time Dependent Heating,”J. Fluid Mech., Vol. 21, pp. 565–576.

    Article  MATH  MathSciNet  Google Scholar 

  • Lee J. D., Choi, C. K. and Yoon, D. Y., 1988, “An Anlaysis of Thermal Convection in a Horizontal Fluid Layer Heated Uniformly from Below,”Proc. 1st KSME-JSME Thermal and Fluid Eng. Conf., Vol. 2, pp. 342–347.

    Google Scholar 

  • Long, R. R., 1976, “The Relation Between Nusselt Number and Rayleigh Number in Turbulent Thermal Convection,”J. Fluid Mech., Vol. 73, pp. 445–451.

    Article  Google Scholar 

  • Morton, B. R., 1957, “On the Equilibrium of a Stratified Layer of Fluid,”J. Mech. Appl. Math., Vol. 10, pp. 433–447.

    Article  MATH  MathSciNet  Google Scholar 

  • Nielsen, R. C. and Sabersky, R. H., 1973, “Transient Heat Transfer in Benard Convection,”Int. J. Heat Mass Transfer, Vol. 16, pp. 2407–2420.

    Article  Google Scholar 

  • Patrick, M. A. and Wragg, A. A., 1975, “Optical and Electrochemical Studies of Transient Free Convection Mass Transfer at Horizontal Surfaces,”Int. J. Heat Mass Transfer, Vol. 18. pp. 1397–1407.

    Article  Google Scholar 

  • Sparrow, E. M., Goldstein, R. J. and Jonsson, V. K., 1964, “Thermal Instability in a Horizontal Fluid Layer: Effect of Boundary Condtions and Nonlinear Temperature Profiles,”J. Fluid Mech., Vol. 18, pp. 513–528.

    Article  MATH  MathSciNet  Google Scholar 

  • Stuart, J. T., 1964, “On Cellular Patterns in Thermal Convection,”J. Fluid Mech., Vol. 18, pp. 481–498.

    Article  MATH  MathSciNet  Google Scholar 

  • Wankat, P. C. and Homsy, G. M., 1977, “Lower Bounds for the Onset Time of Instability in Heated Layers,”Phys. Fluids, Vol. 20, pp. 1200–1201.

    Article  Google Scholar 

  • Yoon, D. Y. and Choi, C. K., 1989, “Thermal Convection in a Staturated Porous Medium subjected to Isothermal Heating,”Korean J. Chem. Eng., Vol. 6, pp. 144–149.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Chemical Engineering, Cheju National University, 690-756, Cheju-do, Korea

    Min Chan Kim

  2. Department of Nuclear and Energy Engineering, Cheju National University, 690-756, Cheju-do, Korea

    Sin Kim

Authors
  1. Min Chan Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sin Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sin Kim.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kim, M.C., Kim, S. The onset of natural convection and heat transfer correlation in horizontal fluid layer heated uniformly from below. KSME International Journal 15, 1451–1460 (2001). https://doi.org/10.1007/BF03185687

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF03185687

Key words

Search

Navigation