Abstract
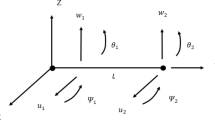
The complex modal testing methods developed for asymmetric rotors are briefly discussed and their performances are experimentally evaluated. For the experiments, a laboratory test rotor is excited by using a newly developed, cost effective magnetic exciter equipped with Hall sensors, which measure the excitation forces. It is concluded that the exciter system is characterized by a wide bandwidth and a high resolution for both the excitation and force measurement, and that the one-exciter/two-sensor technique for complex modal testing of asymmetric rotors is superior to the standard two-exciter/two-sensor technique in terms of practicality and realization.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Abbreviations
- F:
-
Magnetic force
- fy, fz :
-
y- and z- direction force vectors
- g,\(\bar g\),\(\tilde g\) :
-
Complex force vectors in stationary coordinate
- g:
-
Air gap
- Gjw,\(\hat G(j\omega )\),\(\tilde G(j\omega )\):
-
Fourier transforms of g,\(\bar g\) and\(\tilde g\)
- Hgp,\(H_{\hat g\hat p} \),\(H_{\tilde g\tilde p} \):
-
Normal dFRFs
- \(H_{\hat gp} \),\(H_{g\hat p} \):
-
Reverse dFRFs of anisotropic rotors
- \(H_{\tilde gp} \),\(H_{g\tilde p} \):
-
Reverse dFRFs of asymmetric rotors
- \(\tilde H_{ik} i,k = p,g,\hat g,\tilde g\) :
-
Estimated dFRFs using unidirectional excitation
- j:
-
Imaginary number\( = \sqrt { - 1} \)
- k:
-
Stiffness of simple rotor
- p,\(\bar p\):
-
Complex displacement vectors in stationary coordinate
- P(jw),\(\hat P(j\omega )\):
-
Fourier transforms ofp and\(\bar p\)
- S ik ,\(i,k = p,g,\hat g,\tilde g\) :
-
Directional auto- and cross- spectral density functions
- y,z :
-
y- and z- directional displacement vectors
- \(\gamma _{g\hat g}^2 (\gamma _{g\tilde g}^2 )\) :
-
Directional coherence function between g,\(\bar g\) (g,\(\tilde g\))
- Ω :
-
Rotational speed
- \(F(\bar F)\) :
-
Forward (conjugate forward) mode
- \(B(\bar B)\) :
-
Backward (conjugate backward) mode
References
Jei, Y. G. and Lee, C. W., 1988, “Finite Element Model of Asymmetrical Rotor Bearing Systems,”KSME Journal, Vol. 2, No. 2, pp. 116–124.
Lee, C. W., 1991, “A Complex Modal Testing Theory for Rotating Machinery,”Mechanical Systems and Signal Processing, Vol. 5, No. 2, pp. 119–137.
Lee, C. W., 1993,Vibration Analysis of Rotors, Kluwer Academic Publishers.
Lee, C. W. and Kim, J. S., 1992, “Modal Testing and Suboptimal Vibration Control of Flexible Rotor Bearing System by Using a Magnetic Bearing,”ASME J. Dynamic Systems, Measurement and Control, Vol. 114, pp. 244–252.
Gähler, C. and Forch, P., 1994, “A Precise Magnetic Bearing Exciter for Rotordynamic Experiments,”4th Int. Symposium on Magnetic Bearing, Zurich, Switzerland.
Joh, C. Y. and Lee, C. W., 1996, “Use of dFRFs for Diagnosis of Asymmetric/Anisotropic Properties in Rotor-Bearing System,”ASME J. Vibration and Acoustics, Vol. 118, No. 1, pp. 64–69.
Lee, C. W. and Lee, S. K., 1997, “An Efficient Complex Modal Testing Theory for Asymmetric Rotor Systems: Use of Unidirectional Excitation Method,”Journal of Sound and Vibration, Vol. 206, No. 3, pp. 327–338.
Lee, C. W. and Kwon, K. S., 1999, “Identification of Rotating Asymmetry in Rotating Machines by Using Reverse dFRF,”AsME, Design Technical Conference, Las Vegas, DETC99/VIB-8267.
Bendat, J. S. and Piersol, A. G., 1986,Random Data: Analysis and Measurement Procedures, John Wiley & Sons.
Lee, C. W., Yoon, Y. K. and Jeong, H. S., 1997, “Compensation of Tool Axis Misalignment in Active Magnetic Bearing Spindle System,”KSME International Journal, Vol. 11, No. 2, pp. 155–163.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Lee, CW., Kim, SK. Complex modal testing of asymmetric rotors using magnetic exciter equipped with hall sensors. KSME International Journal 15, 866–875 (2001). https://doi.org/10.1007/BF03185265
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF03185265