Abstract
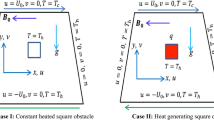
The natural convective heat transfer in a rectangular enclosure with a heating source has been studied by experiment and numerical analysis. The governing equations were solved by a finite volume method, a SIMPLE algorithm was adopted to solve a pressure term. The parameters for the numerical study are positions and surface temperatures of a heating source i.e., Y/H=0.25, 0.5, 0.75 and 11°C≦ΔT≦59°C. The results of isotherms and velocity vectors have been represented, and the numerical results showed a good agreement with experimental values. Based on the numerical results, the mean Nusselt number of the rectangular enclosure wall could be expressed as a function of Grashof number.
Similar content being viewed by others
Abbreviations
- a:
-
Grid space regulation coefficient
- g:
-
Gravity acceleration [m/s2]
- Gr:
-
Grashof number\(\left( {G_r = \frac{{g\beta (T_h - T_c ) H^3 }}{{\nu ^2 }}} \right)\)
- H:
-
Vertical wall length [m]
- K :
-
Turbulent energy [m2/s2]
- L:
-
Horizontal wall length [m]
- Nu:
-
Local Nusselt number\(\left( {Nu = \left. {\frac{{hL}}{k} = \frac{{\partial \theta }}{{\partial X}}} \right|_{X = 0} } \right)\)
- \(\overline {Nu} \) :
-
Mean Nusselt number\(\left( {\overline {Nu} = \frac{1}{L}\int {Nu \cdot dy} } \right)\)
- Pr:
-
Prandtl number
- T:
-
Temperature [°C]
- Th :
-
Heating source temperature [°C]
- Tc :
-
Cooled wall temperature [°C]
- ΔT:
-
Temperature difference [°C]
- U:
-
X direction velocity [m/s]
- V:
-
Y direction velocity [m/s]
- β:
-
Thermal expansion coefficient [K−1]
- δ ij :
-
Kronecker delta
- ε:
-
Turbulent energy dissipation rate
- μ t :
-
Turbulent eddy viscosity [kg/ms]
- ρ:
-
Density [kg/m3]
References
Cheesewright, R., King, K. J. and Ziai S., 1986, “Experimental Data of the Validation of Computer Codes for the Prediction of Two Dimensional Buoyancy Cavity Flow,”Significant Questions in Buoyancy Affected Enclosure or Cavity Flows, ASME-HTD, pp. 75–81.
Chen, Q., van der kooi, J. and Meyers, A., 1988, “Measurement and Computations of Ventilation Efficiency and Temperature Efficiency in a Ventilated Room,”Energy and Buildings, Vol. 12, pp. 85–99.
Chung, H. S., Jeong, H. M., Kim, K. K. and Ro, S. T., 1999, “The Turbulent Natural Convection in Membrane Type LNG Carrier Cofferdam,”Trans. of KSME, Part B, Vol. 23, No. 2, pp. 281–287.
Gebhart, B., Jaluria, Y., Mahajan, R. L. and Sammakia. B., 1988, “Buoyancy-Induced Flows and Transport,”Hemisphere Pub. CO.
Jeong, H. M., Lee, C. J. and Chung, H. S., 2000, “Study on the Numerical Modeling of Turbulent Natural Convection in Rectangular Enclosure,”Trans. of SAREK, Vol. 10, No. 2, pp. 33–39.
Kang, D. K., Kim, W. S. and Lee, K. S., 1995, “A Numerical Study on the Two-Dimensional Turbulent Natural Convection Using a Low-Reynolds Numberk-ε Model,”Trans. of KSME, Vol. 19 No. 3, pp. 741–750.
Kim, T. G. and Sung, H. J., 1993, “A Hybrid Turbulence Model for Prediction of Buoyancy-Driven Turbulent Thermal Convection Flow,”Trans. of KSME, Vol. 17, No. 8, pp. 2069–2078.
Kumar, K., 1983, “Mathematical Modeling of Natural Convection in Fire-a State of the Art Review of the Field Modeling of Variable Density Turbulent Flow,”Fire and Materials, Vol. 103, pp. 456–460.
Lars Davidson, 1990, “Calculation of the Turbulent Buoyancy-Driven Flow in a Rectangular Cavity using an Efficient Solver and Two Different Low Reynolds numberk-ε Turbulence Models,”Numerical Heat Transfer, Part A, Vol. 18, pp. 129–147.
Lee, C. J., Jeong, H. M., Chung, H. S. and Kim, K. K., 1998, “Study on the Natural Convection of Rectangular Enclosure with Heating Source,”Proceeding of KSME, Part B, pp. 417–421.
Lee, J. H., Kim, M. H. and Moh, J. H., 1990, “Natural Convection Heat Transfer in Rectangular Air Enclosure with Adiabatic and Isothermal Horizontal Boundary Condition,”Trans. of KSME, Vol. 14, No. 1, pp. 207–213.
Seo, H. T., Lee, D. S., Yoon, S. H. and Boo, J. S., 1998, “Numerical Analysis on Wall-Attaching Offset Jet with Various Turbulentk-ε Models and Upwind Scheme,”Trans. of KSME, Part B, pp. 828–835.
Shyy, W. and Rao, M. M., 1993, “Simulation of Transient Natural Convection Around an Enclosed Vertical Channel,”Journal of Heat Transfer, ASME, Vol. 115, pp. 946–954.
Suhas, V. Patankar, 1980,Numerical Heat Transfer and Fluid Flow, McGrawhill Co.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Bae, KY., Jeong, HM. & Chung, HS. Study on natural convection in a rectangular enclosure with a heating source. KSME International Journal 18, 294–301 (2004). https://doi.org/10.1007/BF03184739
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF03184739