An implementation of the robust inviscid wall boundary condition in high-speed flow calculations

Abstract

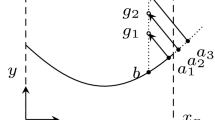
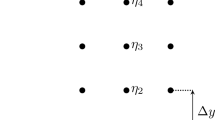
Boundary condition is one of the major factors to influence the numerical stability and solution accuracy in numerical analysis. One of the most important physical boundary conditions in the flowfield analysis is the wall boundary condition imposed on the body surface. To solve a two-dimensional Euler equation, totally four numerical wall boundary conditions should be prescribed. Two of them are supplied by the flow tangency condition. The other two conditions, therefore, should be prepared additionally in a suitable way. In this paper, four different sets of wall boundary conditions are proposed and then applied to solve high-speed flowfields around a quarter circle geometry. A two-dimensional compressible Euler solver is prepared based on the finite volume method. This solver hires three different upwind schemes; Steger-Warming’s flux vector splitting, Roe’s flux difference splitting, and Liou’s advection upstream splitting method. It is found that the way to specify the additional numerical wall boundary conditions strongly affects the overall stability and accuracy of the upwind schemes in high-speed flow calculation. The optimal wall boundary conditions should be also chosen very carefully depending on the numerical schemes used to solve the problem.