Abstract
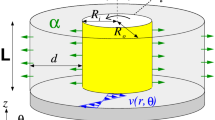
This paper presents our numerical and experimental results of the bifurcation found in Taylor-Couette system with a free surface. The lengths of the two concentric cylinders are finite and their axes are parallel to the direction of the gravitational force. When the end walls of the cylinders are fixed and stationary, numerical and experimental studies have shown that the flow has multiple patterns depending on the cylinder lengths and the Reynolds numbers. Experimental studies on flows with free surfaces also gave various flow modes. Our result shows that the measured and predicted time-dependent displacements of the free surface are in favorable agreement. In case of the cylinder length comparable with the gap width between the cylinders, gradual accelerations of the inner cylinder bring the normal mode flows with one, three and five toroidal vortices. The exchanges of stabilities between these flow modes are summarized in a phase diagram.
Similar content being viewed by others
References
Baier, G. and Graham, M. D., Two-fluid Taylor-Couette flow: experiments and linear theory for immiscible liquids between corotating cylinders, Phys. Fluids, 10–12 (1998), 3045–3055.
Batchelor, G. K., An introduction to fluid dynamics, Chap. 1, (1967), Cambridge Univ. Press.
Bellon, L., Fourten, L., Minassian, V. T. and Rabaud, M., Wave-number selection and parity-breaking bifurcation in directional viscous fingering, Phys. Rev. E, 58-1 (1998), 565–574.
Benjamin, T. B., Bifurcation phenomena in steady flows of a viscous fluid II Experiments, Proc. Roy. Soc. Lond., Ser. A., 359 (1978), 27–43.
Di Prima, R. C. and Swinney, H. L., Instabilities and transition in flow between concentric rotating cylinders, Hydrodynamics instabilities and the transition to turbulence, eds. Swinney H. L. and Gollub J. P., Chap. 6, (1981), Springer.
Fraňa, K., Stiller, J. and Grudmann, R., Taylor-Görtler vortices in the flow driven by a rotating magnetic field in a Cylindrical Container, J. of Visualization, 8-4 (2005), 323–330.
Gelfgat, A. Y., Yarin, A. L., Bar-Yoseph, P. Z., Graham, M. D. and Bai, G., Numerical modeling of two-fluid Taylor-Couette flow with deformable capillary liquid-liquid interface, Phys. Fluids, 16-11 (2004), 4066–4074.
Hantao, J., et al., Hydrodynamic turbulence cannot transport angular momentum effectively in astrophysical disks, Nature, 444-16 (2006), 343–346.
Linek, M. and Ahlers, G., Boundary limitation of wave numbers in Taylor-vortex flow, Phys. Rev. E., 58-3 (1998), 3168–3174.
Michalland, S., Rabaud, M. and Couder, Y., Transition to chaos by spatio-temporal intermittency in directional viscous fingering, Europhysics Lett., 22-1 (1993), 17–22.
Nakamura, I. and Toya, Y., Existence of extra vortex and twin vortex of anomalous mode in Taylor vortex flow with a small aspect ratio, Acta Mechanica, 117 (1996), 33–46.
Nakamura, I., Toya, Y., Yamashita, S. and Ueki, Y., An experiment on a Taylor vortex flow in a gap with a small aspect ratio (instability of Taylor vortex flows), JSME International Journal, Ser. II, 32-3 (1989), 388–394.
Tagg, R., The Couette-Taylor problem, Nonlinear Science Today, 4-3 (1994), 2–25.
Toya, Y., Nakamura, I., Yamashita, S. and Ueki, Y., An experiment on a Taylor vortex flow in a gap with a small aspect ratio — Bifurcation of flows in an asymmetric system —, Acta Mechanica, 102 (1994), 137–148.
Watanabe, T., Furukawa, H. and Nakamura, I., Nonlinear development of flow patterns in an annulus with decelerating inner cylinder, Phys. Fluids, 14-1 (2002), 333–341.
Author information
Authors and Affiliations
Additional information
Takashi Watanabe: He received his Ph.D degree (Eng.) from Nagoya University in 1986. He now works as a professor at the EcoTopia Science Institute, Nagoya University. His current research interests are the computational fluid dynamics of rotating flows and the human-computer interfaces. He is a member of the Japan Society of Mechanical Engineers, the Japan Society of Fluid Mechanics and the Japanese Society for Artificial Intelligence.
Hiroyuki Furukawa: He received the BE degree in mechanical engineering from Nagoya University (1997) and the MA degree and Ph.D degree in human informatics from Nagoya University (1999). He now works as an associate professor at Meijo University. His researches include flow transient, flow visualization and non-linear dynamics.
Yorinobu Toya: He received Ph.D degree (Eng.) from Nagoya University in 1994. He works as a professor at Mechanical Engineering in Nagano National College of Technology. His current researches are the experimental and numerical studies for the circulating flows between rotating cylinders.
Rights and permissions
About this article
Cite this article
Watanabe, T., Furukawa, H. & Toya, Y. Transition of free-surface flow modes in taylor-couette system. J Vis 10, 309–316 (2007). https://doi.org/10.1007/BF03181698
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF03181698