Skip to main content
SpringerLink
Log in

Probability matching priors: a review

  • Published:
Journal of the Italian Statistical Society Aims and scope Submit manuscript

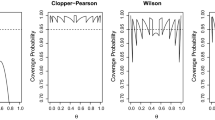
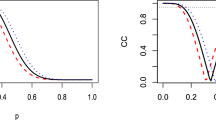
Summary

In recent years, extensive work has been done concerning the derivation of noninformative prior distributions assuring approximate frequentist validity of Bayesian inferences. This paper provides a review of matching priors obtained via quantiles andvia the distribution function. Various matching criteria are described and discussed. Emphasis is laid on a proposal of designing priors matching the true coverage probability as well as the false coverage probabilities of contiguous alternatives with the respective Bayesian counterparts. The review is not primarily meant to be a comprehensive account on the area, but, rather, to convey the main underlying ideas and point out the relationships between matching priors and other noninformative priors, such as the Jeifreys’ and the reference priors.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Bar-Lev, S. K., Reiser, B. (1982), An exponential subfamily which admits UMPU test based on a single test statistic.The Annals of Statistics, 10, 979–989.

    Article  MATH  MathSciNet  Google Scholar 

  • Berger, J. O., Bernardo, J. M. (1989), Estimating a product of means: Bayesian analysis with reference priors.Journal of the American Statistical Association, 84, 200–207.

    Article  MATH  MathSciNet  Google Scholar 

  • Burger, J. O., Bernardo, J. M. (1992a), Ordered group reference priors with application to a multinomial problem.Biometrika, 79, 25–37.

    Article  MathSciNet  Google Scholar 

  • Berger, J. O., Bernardo, I. M. (1992b), Reference priors in a variance components problem. InBayesian Analysis in Statistics and Econometrics (eds. P. K. Goel and N. S. Iyengar), 177–194. New York: Springer-Verlag.

    Google Scholar 

  • Berger, J. O., Bernardo, I. M. (1992c), On the development of reference priors (with discussion). InBayesian Statistics 4 (eds. J. M. Bemardo, J. O. Berger, A. P. Dawid and A. F M. Smith), 35–60. Oxford: Oxford University Press.

    Google Scholar 

  • Berger, J. O., Boukai, B., Wo, Y. (1999), Simultaneous Bayesian-frequentist sequential testing of nested hypotheses.Biometrika, 86, 79–92.

    Article  MATH  MathSciNet  Google Scholar 

  • Berger, J. O., Brown, L. D., Wolpert, R. L. (1994), A unified conditional frequentist and Bayesian test for fixed and sequential simple hypothesis testing.The Annals of Statistics, 22, 1787–1807.

    Article  MATH  MathSciNet  Google Scholar 

  • Berger, J. O., Wolpert, R. L. (1988),The Likelihood Principle, 2nd ed., (ed. S. S. Gupta), IMS, Lecture Notes-Monograph Series. Hayward California.

  • Bernardo, J. M. (1979), Reference posterior distributions for Bayesian inference (with discussion).Journal of the Royal Statistical Society, B, 41, 113–147.

    MATH  MathSciNet  Google Scholar 

  • Bickel, P. J., Ghosh, I. K. (1990), A decomposition for the likelihood ratio statistic and the Bartlett correction — a Bayesian argument.The Annals of Statitics, 18, 1070–1090.

    Article  MATH  MathSciNet  Google Scholar 

  • Cox, D. R., Reid, N. (1987), Parameter orthogonality and approximate conditional inference (with discussion).Journal of the Royal Statistical Society, B, 49, 1–39.

    MATH  MathSciNet  Google Scholar 

  • Datta, G. S. (1996), On priors providing frequentist validity of Bayesian inference for multiple parametric functions.Biometrika, 83, 287–298.

    Article  MATH  MathSciNet  Google Scholar 

  • Datta, G. S., Ghosh, J. K. (1995a), On priors providing frequentist validity for Bayesian inference.Biometrika, 82, 37–45.

    Article  MATH  MathSciNet  Google Scholar 

  • Datta, G. S., Ghosh, J. K. (1995b), Noninformative priors for maximal invariant parameter in group models.Test, 4, 95–114.

    Article  MATH  MathSciNet  Google Scholar 

  • Datta, G. S., Ghosh, M. (1995), Some remarks on noninformative priors.Journal of the American Statistical Association, 90, 1357–1363.

    Article  MATH  MathSciNet  Google Scholar 

  • Datta, G. S., Ghosh, M. (1996), On the invariance of noninformative priors.The Annals of Statistics, 24, 141–159.

    Article  MATH  MathSciNet  Google Scholar 

  • Dawid, A. P., Stone, M., Zidek, J. V. (1973), Marginalization paradoxes in Bayesian and structural inference (with discussion).Journal of the Royal Statistical Society, B, 35, 189–233.

    MATH  MathSciNet  Google Scholar 

  • Garvan, C. W., Ghosh, M. (1997), Noninformative priors for dispersion models.Biometrika, 84, 976–982.

    Article  MATH  MathSciNet  Google Scholar 

  • Garvan, C. W., Ghosh, M. (1999), On the property of posteriors for dispersion models.Journal of Statistical Planning and Inference, 78, 229–241.

    Article  MATH  MathSciNet  Google Scholar 

  • Ghosh, M., Carlin, B. P., Srivastava, M. S. (1995), Probability matching priors for linear calibration.Test, 4, 333–357.

    Article  MATH  MathSciNet  Google Scholar 

  • Ghosh, J. K., Mukerjee, R. (1991), Characterization of priors under which Bayesian and frequentist Bartlett corrections are equivalent in the multiparameter case.Journal of Multivariate Analysis, 38, 385–393.

    Article  MATH  MathSciNet  Google Scholar 

  • Ghosh, J. K., Mukerjee, R. (1992a), Bayesian and frequentist Bartlett corrections for likelihood ratio and conditional likelihood ratio tests.Journal of the Royal Statistical Society, B, 54, 867–875.

    MathSciNet  Google Scholar 

  • Ghosh, J. K., Mukerjee, R. (1992b), Non-informative priors (with discussion). InBayesian Statistics 4 (eds. J. M. Bernardo, J. O. Berger, A. P. Dawid and A. F. M. Smith), 195–210. Oxford: Oxford University Press.

    Google Scholar 

  • Ghosh, J. K., Mukerjee, R. (1993a), Frequentist validity of highest posterior density regions in the multiparameter case.Annals of the Institute of Statistical Mathematics, 45, 293–302.

    Article  MATH  MathSciNet  Google Scholar 

  • Ghosh, J. K., Mukerjee, R. (1993b), On priors that match posterior and frequentist distribution functions.The Canadian Journal of Statistics; 21, 89–96.

    Article  MATH  MathSciNet  Google Scholar 

  • Ghosh, J. K., Mukerjee, R. (1995), Frequentist validity of highest posterior density regions in the presence of nuisance parameters.Statistics and Decisions, 13, 131–139.

    MATH  MathSciNet  Google Scholar 

  • Hartigan, J. A. (1983),Bayes Theory. New York: Springer-Verlag.

    MATH  Google Scholar 

  • Jeffreys, H. (1946), An invariant form for the prior probability in estimation problems. InProceedings of the Royal Society of London, A, 186, 453–461.

  • Jeffreys, H. (1961),Theory of Probability, 3rd ed. Oxford: Oxford University Press.

    MATH  Google Scholar 

  • Johnson, R. A. (1970), Asymptotic expansions associated with posterior distributions.The Annals of Mathematical Statistics, 41, 851–864.

    Article  MATH  Google Scholar 

  • Kass, R. E., Wasserman, L. A. (1996), The selection of prior distributions by formal rules.Journal of the American Statistical Association, 91, 1343–1370.

    Article  MATH  Google Scholar 

  • Mukerjee, R., Dey, D. K. (1993), Frequentist validity of posterior quantiles in the presence of a nuisance parameter: higher order asymptotics.Biometrika, 80, 499–505.

    Article  MATH  MathSciNet  Google Scholar 

  • Mukerjee, R., Ghosh, M. (1997), Second-order probability matching priors.Biometrika 84, 970–975.

    Article  MATH  MathSciNet  Google Scholar 

  • Mukerjee, R., Reid, N. (1999), On a property of probability matching priors: matching the alternative coverage probabilities.Biometrika, 86, 333–340.

    Article  MATH  MathSciNet  Google Scholar 

  • Neyman, J., Scorr, E. L. (1948), Consistent estimates based on partially consistent observations.Econometrica, 16, 1–32.

    Article  MathSciNet  Google Scholar 

  • Nicolaou, A. (1993), Bayesian intervals with good frequentist behaviour in the presence of nuisance parameters.Journal of the Royal Statistical Society, B, 55, 377–390.

    MATH  MathSciNet  Google Scholar 

  • Peers, H. W. (1965), On confidence points and Bayesian probability points in the case of several parameters.Journal of the Royal Statistical Society, B, 27, 9–16.

    MATH  MathSciNet  Google Scholar 

  • Peers, H. W. (1968), Confidence properties of Bayesian interval estimates.Journal of the Royal Statistical Society, B, 30, 535–544.

    MATH  MathSciNet  Google Scholar 

  • Regazzini, E. (1983),Sulle probabilità coerenti net senso di de Finetti. Bologna: CLUEB.

    Google Scholar 

  • Reid, N. (1995), Likelihood and Bayesian approximation methods (with discussion). InBayesian Statistics 5 (eds. J. M. Bernardo, J. O. Berger, A. P. Dawid and A. F. M. Smith), 351–368. Oxford: Oxford University Press.

    Google Scholar 

  • Rousseau, J. (1997),Étude des propértiés asymptotiques des estimateurs de Bayes. Université Paris 6, Ph.D. thesis.

  • Stein, C. (1965), Approximation of improper prior measures by prior probability measures. InBernoulli-Bayes-Laplace Anniversary Volume: Proceedings of an International Research Seminar Statistical Laboratory (eds. J. Neyman and L. M. Le Cam), 217- 240. New York: Springer-Verlag.

    Google Scholar 

  • Stein, C. (1985), On the coverage probability of confidence sets based on a prior distribution. InSequential Methods in Statistics, Banach Center Publications, 16, 485–514. Warsaw: PWN-Polish Scientific Publishers.

    Google Scholar 

  • Sun, D. (1994), Integrable expansions for posterior distributions for a two-parameter exponential family.The Annals of Statistics, 22, 1808–1830.

    Article  MATH  MathSciNet  Google Scholar 

  • Sun, D. (1997), A note on noninformative priors for Weibull distributions.Journal of Statistical Planning and Inference, 61, 319–338.

    Article  MATH  MathSciNet  Google Scholar 

  • Sun, D., Ghosh, M., Basu, A. P. (1998), Bayesian analysis for a stress-strength system under noninformative priors.The Canadian Journal of Statistics, 26, 323–332.

    Article  MATH  MathSciNet  Google Scholar 

  • Sun, D., Ye, K. (1996), Frequentist validity of posterior quantiles for a two-parameter exponential family.Biometrika, 83, 55–65.

    Article  MATH  MathSciNet  Google Scholar 

  • Sweeting, T. J. (1995), A framework for Bayesian and likelihood approximations in statistics.Biometrika, 82, 1–23.

    Article  MATH  MathSciNet  Google Scholar 

  • Tibshirani, R. (1989), Noninformative priors for one parameter of many.Biometrika, 76, 604–608.

    Article  MATH  MathSciNet  Google Scholar 

  • Welch, B. L. (1965), On comparisons between confidence point procedures in the case of a single parameter.Journal of the Royal Statistical Society B, 27, 1–8.

    MATH  MathSciNet  Google Scholar 

  • Welch, B. L., Peers, H. W. (1963), On formulae for confidence points based on integrals of weighted likelihoods.Journal of the Royal Statistical Society B, 25, 318–329.

    MATH  MathSciNet  Google Scholar 

  • Woodroofe, M. (1986), Very weak expansions for sequential confidence intervals.The Annals of Statistics, 14, 1049–1067.

    Article  MATH  MathSciNet  Google Scholar 

  • Woodroofe, M. (1989), Very weak expansions for sequentially designed experiments: linear models.The Annals of Statistics, 17, 1087–1102.

    Article  MATH  MathSciNet  Google Scholar 

  • Ye, K. (1993), Reference priors when the stopping rule depends on the parameter of interest.Journal of the American Statistical Association, 88, 360–363.

    Article  MATH  MathSciNet  Google Scholar 

  • Yin, M. (1998), Asymptotic expansions for posterior probability in regression model.Statistics and Decisions, 16, 349–368.

    MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dipartimento di Scienze Statistiche, Università di Padova, Via Cesare Battisti, 241-243, I-35121, Padova, Italy

    Catia Scricciolo

Authors
  1. Catia Scricciolo
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Scricciolo, C. Probability matching priors: a review. J. Ital. Statist. Soc. 8, 83 (1999). https://doi.org/10.1007/BF03178943

Download citation

  • DOI: https://doi.org/10.1007/BF03178943

Keywords

Search

Navigation