Skip to main content
SpringerLink
Log in

A construction method for data adapted wavelet

  • Published:
Japan Journal of Industrial and Applied Mathematics Aims and scope Submit manuscript

Abstract

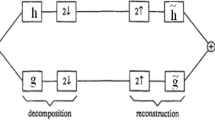
A construction method is proposed for a biorthogonal wavelet which approximates an arbitrarily given target function. This method is expected to be useful in the cases where the given data is a superposition of the target functions dilated and translated. The biorthogonal wavelet then provides an efficient decomposition of the given data into the elements of events. The biorthogonal wavelet is obtained by Lagrange’s multiplier method minimizing the L2-norm of the difference between the target function and the primary wavelet. As an example, this method is applied to the Mexican hat function as a target function, to produce a biorthogonal wavelet close to the Mexican hat.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. K. Amaratunga, et al., Wavelet-Galerkin solutions for one dimensional partial differential equation. IESL Report MIT, Order No.92-05, 1992.

  2. C. Basdevant, M. Holschneider and V. Perrier, Methode des ondelettes mobiles. C. R. Acad. Sci. Paris,310 Serie I (1990), 647–652.

    MATH  MathSciNet  Google Scholar 

  3. S. Dahlke and I. Weinreich, Wavelet-Galerkin methods: An adapted biorthogonal wavelet basis. Constructive Approximation,9 (1993), 237–262.

    Article  MATH  MathSciNet  Google Scholar 

  4. I. Daubechies, Ten Lectures on Wavelets. CBMS-NSF Series in Applied Mathematics61, SIAM Publ., Philadelphia, 1992.

    Google Scholar 

  5. M. Farge, Wavelet transforms and their applications to turbulence. Annual Rev. Fluid Mech.,24 (1992), 395–457.

    Article  MathSciNet  Google Scholar 

  6. R. Glowinski, et al., Wavelet solution of linear and nonlinear elliptic, parabolic and hyperbolic problems in one space dimension. Aware Inc. Technical Report, AD890527. 1, 1989, 1–79.

    MathSciNet  Google Scholar 

  7. T. Irino and H. Kawahara, Signal reconstruction from modified wavelet transform. IEEE Proceedings of ICASSP-92, 1992.

  8. H. Kikuchi, et al., Fast nonorthogonal wavelet transforms and reconstructions for detonation detection. IEEE International Symp. Circuits and Systems (Vol. 1), 1993, 503–506.

    Google Scholar 

  9. L. Jameson, On the spline-based wavelet differentiation matrix. Appl. Numer. Math.,17, No. 1 (1995), 33–45.

    Article  MATH  MathSciNet  Google Scholar 

  10. A. Latto and E. Tenenbaum, Compactly supported wavelets and the numerical solution of Burger’s equation. C. R. Acad. Sci. Paris,311 Serie I (1990), 903–909.

    MATH  MathSciNet  Google Scholar 

  11. A.S. Lewis and G. Knowles, Video compression using 3D wavelet transforms. Electron. Lett.,26, No. 6 (1990), 396–398.

    Article  Google Scholar 

  12. Y. Maday, V. Perrier and J.C. Ravel, Dynamical adaptivity using wavelets basis for the approximation of partial differential equations. C. R. Acad. Sci. Paris,312 Serie I (1991), 405–410.

    MATH  MathSciNet  Google Scholar 

  13. S.G. Mallat, Multiresolution approach to wavelets in computer vision. Wavelets, Springer, 1989, 313–327.

    Google Scholar 

  14. S.G. Mallat, A Wavelet Tour of Signal Processing. Academic Press, 1998, 265.

  15. J. Morlet, et al., Wave propagation and sampling theory. Geophysics,47, No. 2 (1982), 203–236.

    Article  Google Scholar 

  16. S. Qian and J. Weiss, Wavelets and the numerical solution of partial differential equations. J. Comput. Phys.,106, No. 3 (1993), 155–175.

    Article  MATH  MathSciNet  Google Scholar 

  17. F. Sasaki and M. Yamada, Biorthogonal wavelets adapted to integral operators and their applications. Japan J. Indust. Appl. Math.,14, No. 2 (1997), 257–277.

    Article  MathSciNet  Google Scholar 

  18. A.K. Soman, P.P. Vaidyanathan and T.Q. Nguyen, Linear phase orthonormal filter banks. IEEE Proceedings of ICASSP-93 (Vol. 3), 1993, 209–212.

    Google Scholar 

  19. M. Vetterli, Signal expansions for compression. IEEE Proceedings of 1994 Workshop on Information Theory and Statistics, 1994.

  20. J. Weiss, Wavelets and the study of two dimensional turbulence. Aware Inc. Technical Report, AD910628, 1991, 1–28.

  21. J.R. Williams and K. Amaratunga, O(n) multiscale wavelet solvers with arbitrarily high accuracy. IESL Report MIT, Order No.93-24, 1993.

  22. M. Yamada and K. Ohkitani, Orthonormal wavelet analysis of turbulence. Fluid Dynamics Research,8 (1991), 101–115.

    Article  Google Scholar 

  23. K. Yomogida, Detection of anomalous seismic phases by the wavelet transform. Geophys. J. Int.,116 (1994), 119–130.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Graduate School of Mathematical Sciences, University of Tokyo, 3-8-1 Komaba, Meguroku, 153-8914, Tokyo, Japan

    Michio Yamada

  2. I. T. Solutions Department, Kajima Corporation, 5-30 Akasaka 6-chome, Minatoku, 107-8502, Tokyo, Japan

    Fumio Sasaki

Authors
  1. Michio Yamada
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fumio Sasaki
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Michio Yamada.

About this article

Cite this article

Yamada, M., Sasaki, F. A construction method for data adapted wavelet. Japan J. Indust. Appl. Math. 18, 307–320 (2001). https://doi.org/10.1007/BF03168577

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF03168577

Key words

Search

Navigation