Abstract
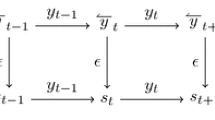
In this paper we discuss a dimensional explanation of the channel capacity and the ambiguity in information theory, which characterize the channel through which infinite sequences whose each coordinate takes values in alphabet are transmitted. Infinite sequences are put into the channel, transmitted and received as output sequences. Since the channel has memory and noise, the output sequences are not necessarily the same to the input sequences. Output sequences are ambiguous.
In this paper for the first time we discuss relationships between an ergodic channel capacity and the Hausdorff dimension of the set of all the output sequences for a noisy channel with finite memory and show that the former is less than or equal to the latter. For each output sequence the ambiguity set is defined to be the set of all the input sequences transmitted to the output sequence. The ambiguity is defined to be a quantity characterizing the complexity of an ambiguity set. Hausdorff dimension is also another quantity characterizing the complexity of the ambiguity set. In this paper we also consider relationships between an ambiguity and Hausdorff dimension of an ambiguity set for a noiseless channel with memory 2, and show that the Hausdorff dimension equals to the ambiguity.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
P. Billingsley, Ergodic Theory and Information. Wiley, New York, 1965.
W.M. Conner, The capacity and ambiguity of a transducer. Ann. Math. Statis.,41, No. 6 (1970), 2093–2104.
H.G. Eggleston, The fractional dimension of a set defined by decimal properties. Quart. J. Math. Oxford Ser.(2),20 (1949), 31–36.
B.P. Yakov, Dimension Theory in Dynamical Systems. University of Chicago Press, 1997.
A.S. Besicovitch, On the sum of digits of numbers represented in the dyadic system. Math. Ann.,110 (1935), 321–330.
H.G. Eggleston, Set of fractal dimention which occur in some problems of number theory. Proc. London Math. Soc.,54 (1952), 42–93.
J.R. Kinney, Singular functions associated with Markov chains. Proc. Amer. Math. Soc.,9 (1958), 603–608.
H. Dym, On a class of monotone functions generated by ergodic sequences. Amer. Math. Monthly,75 (1968), 594–601.
W. Feller, An Introduction to Probability Theory and Its Applications (Vol. II). John Wiley, 1971.
K.J. Falconer, The Geometry of Fractal Sets. Cambring University Press, 1985.
L. Breiman, On achieving channel capacity in finite-memory channels. Illinois J. Math.,4 (1960), 246–252.
Author information
Authors and Affiliations
Corresponding author
About this article
Cite this article
Suzuki, T., Ohi, F. & Kowada, M. Dimensional explanation of capacity and ambiguity in information theory. Japan J. Indust. Appl. Math. 19, 347–375 (2002). https://doi.org/10.1007/BF03167484
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF03167484