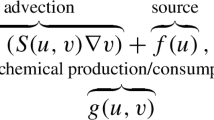Skip to main content
SpringerLink
Log in

Dynamics of metastable localized patterns and its application to the interaction of spike solutions for the Gierer-Meinhardt systems in two spatial dimensions

Dedicated to Professor Masayasu Mimura on his sixtieth birthday

  • Published:
Japan Journal of Industrial and Applied Mathematics Aims and scope Submit manuscript

Abstract

In this paper, the Gierer-Meinhardt model systems with finite diffusion constants in the whole spaceR 2 is considered. We give a regorous proof on the existence and the stability of a single spike solution, and by using such informations, the repulsive dynamics of the interacting multi single-spike solutions is also shown when distances between spike solutions are sufficiently large. This clarifies some part of the mechanism of the evolutional process of localized patterns appearing in the Gierer-Meinhardt model equations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. N.D. Alikakos and G. Fusco, Slow dynamics for the Cahn-Hilliard equation in higher spatial dimensions: the motion of bubbles. Arch. Rat. Mech.,141 (1998), 1–61.

    Article  MATH  MathSciNet  Google Scholar 

  2. P. Bates and G. Pusco, Equilibria with many nuclei for the Cahn-Hilliard equation. J. Diff. Eqns.,160 (1999), 283–356.

    Article  Google Scholar 

  3. P. Bates, K. Lu and C. Zeng, Approximate invariant manifolds for infinite dimensional dynamical systems. Preprint.

  4. G. Bellettini and G. Pusco, Stable dynamics of spikes in solutions to a system of activator-inhibitor type. Preprint.

  5. P. Bates, E.N. Dancer and J. Shi, Multi-spike stationary solutions of the Cahn-Hilliard equation in higher-dimension and instability. Adv. Diff. Eqns.,4 (1999), 1–69.

    MATH  MathSciNet  Google Scholar 

  6. X. Chen and M. Kowalczyk, Slow dynamics of interior spikes in the shadow Gierer-Meinhardt system. Preprint.

  7. K.-S. Cheng and W.-M. Ni, On the structure of the conformai Gaussian curvature equation onR 2. Duke Math. J.,62 (1991), 721–737.

    Article  MATH  MathSciNet  Google Scholar 

  8. M. del Pino, P. Felmer and J. Wei, On the role of mean curvature in some singularly perturbed Neumann problems. Comm. PDE,25 (2000), 155–177.

    Article  MATH  Google Scholar 

  9. W.-Y. Ding and W.-M. Ni, On the elliptic equation Δu+ ϰun+2/n−2 = 0 and related topics. Duke Math. J.,52 (1985), 485–506.

    Article  MATH  MathSciNet  Google Scholar 

  10. S.-I. Ei, The montion of weakly interacting pulses in reaction-diffusion systems. J. Dynamics and Diff. Eqns.,14 (2002), 85–137.

    Article  MATH  MathSciNet  Google Scholar 

  11. S.-I. Ei and M. Mimura, Particle like behavior of pulses in reaction-diffusion systems, in prepararion.

  12. S.-I. Ei and J. Wei, in preparation.

  13. C. Gui and N. Ghoussoub, Multi-peak solutions for a semilinear Neumann problem involving the critical Sobolev exponent. Math. Zeit.,229 (1998), 443–474.

    Article  MATH  MathSciNet  Google Scholar 

  14. C. Gui, Multi-peak solutions for a semilinear Neumann problem. Duke Math. J.,84 (1996), 739–769.

    Article  MATH  MathSciNet  Google Scholar 

  15. B. Gidas, W.-M. Ni and L. Nirenberg, Symmetry of positive solutions of nonlinear elliptic equations inR N. Adv. Math. Suppl. Stud.,7A (1981), 369–402.

    MathSciNet  Google Scholar 

  16. A. Gierer and H. Meinhardt, A theory of biological pattern formation. Kybernetik,12 (1972), 30–39.

    Article  Google Scholar 

  17. C. Gui and J. Wei, Multiple interior peak solutions for some singularly perturbed Neumann problems. J. Diff. Eqns.,158 (1999), 1–27.

    Article  MATH  MathSciNet  Google Scholar 

  18. C. Gui, J. Wei and M. Winter, Multiple boundary peak solutions for some singularly perturbed Neumann problems. Ann. Inst. H. Poincaré Anal. Non Linéaire,17 (2000), 47–82.

    Article  MATH  MathSciNet  Google Scholar 

  19. D. Iron and M. J. Ward, A metastable spike solution for a non-local reaction-diffusion model. SIAM J. Appl. Math.,60 (2000), 778–802.

    Article  MATH  MathSciNet  Google Scholar 

  20. M.K. Kwong and L. Zhang, Uniqueness of positive solutions of Δu+ ƒ (u) = 0 in an annulus. Diff. Integ. Eqns.,4 (1991), 583–599.

    MATH  MathSciNet  Google Scholar 

  21. M. Kowalczyk, Multiple spike layers in the shadow Gierer-Meinhardt system: existence of equilibria and approximate invariant manifold. Duke Math. J.,98 (1999), 59–111.

    Article  MATH  MathSciNet  Google Scholar 

  22. Y.-Y. Li, On a singularly perturbed equation with Neumann boundary condition. Comm. PDE.,23 (1998), 487–545.

    MATH  Google Scholar 

  23. W.-M. Ni and I. Takagi, On the shape of least energy solution to a semilinear Neumann problem. Comm. Pure Appl. Math.,41 (1991), 819–851.

    Article  MathSciNet  Google Scholar 

  24. W.-M. Ni and I. Takagi, Locating the peaks of least energy solutions to a semilinear Neumann problem. Duke Math. J.,70 (1993), 247–281.

    Article  MATH  MathSciNet  Google Scholar 

  25. W.-M. Ni and I. Takagi, Point-condensation generated by a reaction-diffusion system in axially symmetric domains. Japan J. Indust. Appl. Math.,12 (1995), 327–365.

    Article  MATH  MathSciNet  Google Scholar 

  26. W.-M. Ni, I. Takagi and E. Yanagida, Tohoku Math. J., to appear.

  27. W.-M. Ni and J. Wei, On the location and profile of spike-layer solutions to singularly perturbed semilinear Dirichlet problems. Comm. Pure Appl. Math.,48 (1995), 731–768.

    Article  MATH  MathSciNet  Google Scholar 

  28. W.-M. Ni, Diffusion, cross-diffusion, and their spike-layer steady states. Notices of Amer. Math. Soc.,45 (1998), 9–18.

    MATH  Google Scholar 

  29. A. Turing, The chemical basis of morphogenesis. Phil. Trans. Roy. B.,237 (1952), 37–72.

    Article  Google Scholar 

  30. M. J. Ward, An asymptotic analysis of localized solutions for some reaction-diffusion models in multi-dimensional domains. Studies in Appl. Math.,97 (1996), 103–126.

    MATH  Google Scholar 

  31. M.J. Ward, Metastable bubble solutions for the Allen-Cahn equation with math conservation. SIAM J. Appl. Math.,56 (1996), 1247–1279.

    Article  MATH  MathSciNet  Google Scholar 

  32. J. Wei, On the construction of single-peaked solutions to a singularly perturbed semilinear Dirichlet problem. J. Diff. Eqns.,129 (1996), 315–333.

    Article  MATH  Google Scholar 

  33. J. Wei, On the boundary spike layer solutions of singularly perturbed semilinear Neumann problem. J. Diff. Eqns.,134 (1997), 104–133.

    Article  MATH  Google Scholar 

  34. J. Wei, On the interior spike layer solutions for some singular perturbation problems. Proc. Royal Soc. Edinburgh, Section A (Mathematics),128 (1998), 849–874.

    MATH  Google Scholar 

  35. J. Wei, On the interior spike layer solutions of singularly perturbed semilinear Neumann problem. Tohoku Math. J.,50 (1998), 159–178.

    Article  MATH  MathSciNet  Google Scholar 

  36. J. Wei, Uniqueness and eigenvalue estimates of boundary spike solutions. Proc. Royal Soc. Edinburgh, Section A (Mathematics), to appear.

  37. J. Wei, On single interior spike solutions of Gierer-Meinhardt system: uniqueness, spectrum estimates and stability analysis. Eur. J. Appl. Math.,10 (1999), 353–378.

    Article  MATH  Google Scholar 

  38. J. Wei, Existence, stability and metastability of point condensation patterns generated by Gray-Scott system. Nonlinearity,12 (1999), 593–616.

    Article  MATH  MathSciNet  Google Scholar 

  39. J. Wei, Pattern formation two-dimensional Gray-Scott model: existence of single spot solutions and their stability. Physica D,148 (2001), 20–48.

    Article  MATH  MathSciNet  Google Scholar 

  40. J. Wei and M. Winter, Stationary solutions for the Cahn-Hilliard equation. Ann. Inst. H. Poincaré Anal. Non Linéaire,15 (1998), 459–492.

    Article  MATH  MathSciNet  Google Scholar 

  41. J. Wei and M. Winter, Multiple boundary spike solutions for a wide class of singular perturbation problems. J. London Math. Soc.,59 (1999), 585–606.

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Graduate School of Integ, Sci., Yokohama City University, 22-2 Seto, Kanazawa-ku, 236-0027, Yokohama, Japan

    Shin-Ichiro Ei

  2. Department of Mathematics, Chinese University of Hong Kong, Shatin, N.T., Hong Kong

    Juncheng Wei

Authors
  1. Shin-Ichiro Ei
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Juncheng Wei
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Shin-Ichiro Ei or Juncheng Wei.

About this article

Cite this article

Ei, SI., Wei, J. Dynamics of metastable localized patterns and its application to the interaction of spike solutions for the Gierer-Meinhardt systems in two spatial dimensions. Japan J. Indust. Appl. Math. 19, 181–226 (2002). https://doi.org/10.1007/BF03167453

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF03167453

Key words

Search

Navigation