Abstract
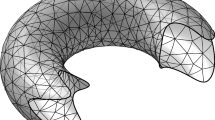
We concern ourselves with the finite element approximations of the partial differential equation: ∂2 u/∂x 2 + ∂2 u/∂y 2 -qu =f (z =x +iy) on a compact bordered Riemann surface\(\bar \Omega \). It is characteristic of our method that we adopt ordinary triangular meshes and linear elements on a subregion of every fixed parameter disk, our triangulation embeds\(\bar \Omega \) exactly even in the case of curvilinear boundary arcs, and our approximating functions ofu express singular property exactly near inner and corner singularities. We obtain the error estimates for finite element approximations and also apply our results to numerical calculation of some boundary value problems.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
L.V. Ahlfors and L. Sario, Riemann Surfaces. Princeton University Press, Princeton, 1960.
I. Babuška, The rate of convergence for the finite element method. SIAM J. Numer. Anal.,8 (1971), 304–315.
I. Babuška and R.B. Kellogg, Nonuniform error estimates for the finite element method. SIAM J. Numer. Anal.,12 (1975), 868–875.
I. Babuška, R.B. Kellogg and J. Pitkäranta, Direct and inverse error estimates for finite elements with mesh refinements. Numer. Math.,33 (1979), 447–471.
I. Babuška, B.A. Szabo and I.N. Katz, The p-version of the finite element method. SIAM J. Numer. Anal.,18 (1981), 515–545.
R.E. Bank and T. Dupont, An optimal order process for solving finite element equations. Math. Comp.,36 (1981), 35–51.
R.E. Bank, T.F. Dupont and H. Yserentant, The hierarchical basis multigrid method. Numer. Math.,52 (1988), 427–458.
H. Blum and R. Rannacher, Extrapolation techniques for reducing the pollution effect of reentrant corners in the finite element method. Numer. Math.,52 (1988), 539–564.
J.H. Bramble and M. Zlámal, Triangular elements in the finite element method. Math. Comp.,24 (1970), 809–820.
D. Gilbarg and N.S. Trudinger, Elliptic Partial Differential Equations of Second Order (2nd Edition). Springer-Verlag, Berlin-Heidelberg-New York-Tokyo, 1983.
P. Grisvard, Singularities in Boundary Value Problems. Masson, Paris, 1992.
B.Q. Guo, The h-p version of the finite element method for elliptic equations of order 2m. Numer. Math.,53 (1988), 199–224.
H. Hara and H. Mizumoto, Determination of the modulus of quadrilaterals by finite element methods. J. Math. Soc. Japan,42 (1990), 295–326.
H. Mizumoto, A finite-difference method on a Riemann surface. Hiroshima, Math. J.,3 (1973), 277–332.
H. Mizumoto and H. Hara, Finite element approximations of harmonic differentials on a Riemann surface. Hiroshima Math. J.,18 (1988), 617–654.
H. Mizumoto and H. Hara, Maximum principles for finite element solutions on a Riemann surface, II. Kawasaki Medical Welfare J.,3 (1993), 183–192.
H. Mizumoto and H. Hara, Determination of the moduli of ring domains by finite element methods. Int. J. Differential Equations and Applications,3 (2001), 325–337.
I.N. Molchanov and E.F. Galba, On finite element methods for the Neumann problem. Numer. Math.,46 (1985), 587–598.
C.B. Morrey, Jr., Multiple Integrals in the Calculus of Variations. Springer-Verlag, Berlin-Heidelberg-New York, 1966.
A.H. Schatz and L.B. Wahlbin, Interior maximum norm estimates for finite element methods. Math. Comp.,31 (1977), 414–442.
G. Strang and G.J. Fix, An Analysis of the Finite Element Method. Prentice-Hall, Englewood Cliffs, 1973.
L.B. Wahlbin, Local behavior in finite element methods. Handbook of Numerical Analysis, Vol.11 (eds. P. G. Ciarlet and J. L. Lions), Elsevier Science Publishers B. V., North-Holland, 1991, 355–522.
Author information
Authors and Affiliations
Corresponding author
About this article
Cite this article
Hara, H., Mizumoto, H. Finite element approximations forΔu −qu = f on a Riemann surface. Japan J. Indust. Appl. Math. 19, 113–141 (2002). https://doi.org/10.1007/BF03167450
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF03167450