Approximations of functionals of some modulated-Poisson Voronoi tessellations with applications to modeling of communication networks

Abstract

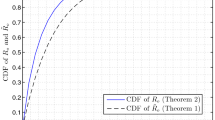
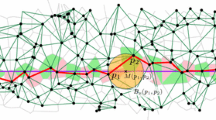
We consider the Voronoi tessellation of Euclidian plane that is generated by an inhomogeneous Poisson point process whose intensity takes different constant values on sets of some finite partition of the plane. We show that mean functionals of a cell with the nucleus located in a given set of the partition can be approximated by the mean functionals of the typical cell of the homogeneous Poisson Voronoi tessellation with intensity appropriate to this partitioning set. We give bounds for the approximation errors, which depend on the distance of the nucleus to the boundary of the element of the partition it belongs to. In the case of a stationary random partition, we show that mean functionals of the typical cell of the respective double-stochastic Poisson-Voronoi tessellation admit an approximate decomposition formula. The true value is approximated by a mixture of respective mean functionals for homogeneous models, while the explicit upper bound for the remaining term, which depends on the covariance functions of the random partitioning elements, can be computed numerically for a large class of practical examples. This paper complements the previous studies in [9], where the distribution of the typical cell is approximated. One of the motivations for the study in question is modeling of modern communication networks, where application of the Poisson Voronoi tessellation has already proven to give some interesting results and where the assumption of the homogeneity is often non-adequate.