Comparison of conventional and “invariant” schemes of fundamental solutions method for annular domains

Abstract

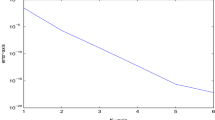
This is a mathematical study of the fundamental solutions method (or the charge simulation method) for a two-dimensional Dirichlet problem: Δu = 0 inΩ,u| _∂Ω =f for an annular domainΩ = {x ∈R ² | ρ₁ < ∥x∥ < ρ₂}, where the boundary dataf is assumed to have exponentially decaying Fourier coefficients. Emphasis is laid on the comparison of the conventional scheme and the “invariant” scheme; the former adopts$u^{(N)} (x) = - \frac{1}{{2\pi }}\sum\nolimits_{j = 1}^N {Q_j \log \left\| {x - y_j } \right\|}$ (where y _j ∈R ²-Ω (j=1, …,N) are charge points) and the latter uses$u^{(N)} (x) = Q_0 - \frac{1}{{2\pi }}\sum\nolimits_{j = 1}^N {Q_j \log \left\| {x - y_j } \right\|}$ with coefficientsQ _j (j=0,1, …,N) subject to$\sum\nolimits_{j = 1}^N {Q_j = 0}$ (the “invariant” scheme, proposed recently by the author, remains invariant with respect to trivial affine transformations in the problem description). When the charge points are distributed with natural symmetry on the circles ‖y‖=R ₁,R ₂ (whereR ₁ <ρ ₁ <ρ ₂ < R₂) and the collocation points are on the circles ‖x‖ =ρ ₁,ρ ₂, it is found that the conventional scheme converges exponentially to the true solution with the increase ofN providedR ₂ ≠ 1, whereas exponential convergence is always the case with the “invariant” scheme (irrespective ofR ₂) The results show that the “invariant” scheme is not only physically but also mathematically nicer than the conventional scheme.