Abstract
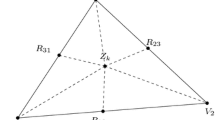
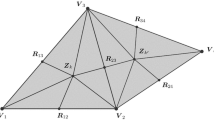
Let Δ mn be a grid partition of curves that divide a rectangular domain into a finite or countable number of cells inR 2, called type-1 triangulations. A kind of bivariate cubic splines is considered. A class of linear spline operators based on the bivariate cubic splines on the partition is given and shown to satisfy the identities about certain polynomials. In addition, these identities enable us to give error estimates for approximation from the entire space of the cubic spline function with the grid partition Δ mn .
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
C.K. Chui, L.L. Schumaker and R.-H. Wang, On space of piecewise polynomials with boundary conditions II, Type-1 triangulations. Approximation Theory, CMS Conf. Proc. of Amer. Math. Soc., Vol.3, 1983, 51–66.
C.K. Chui and R.-H. Wang, Spaces of bivariate cubic and quartic splines on type-1 triangulations. J. Math. Anal. Appl.,101 (1984), 540–554.
C.K. Chui and R.-H. Wang, On a bivariate B-spline basis. Scientia Sinica (Series A),27, No.11 (1984), 1129–1142.
C.K. Chui and R.-H. Wang, ConcerningC 1 B-splines on triangulations of non-uniform rectangular partition. J. Approx. Theory Appl.,1, No.1 (1984), 11–18.
P.O. Predrickson, Generalized triangular splines. Lakehead University, Math. Report No. 7-17, 1971.
R.-H. Wang, On the analysis of multivariate splines in the case of arbitrary partition. Scientia Sinica. Math.I (1979), 215–226.
R.-H. Wang, The dimension and basis of spaces of multivariate splines. J. Comput. Appl. Math.,12 &13 (1985), 163–177.
Author information
Authors and Affiliations
About this article
Cite this article
Zhang, S.L., Wang, R.H., Oyanagi, Y. et al. A kind of bivariate cubic splines and related linear operators on type-1 triangulation. Japan J. Indust. Appl. Math. 17, 391–402 (2000). https://doi.org/10.1007/BF03167374
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF03167374