Abstract
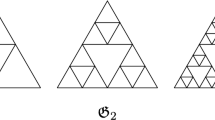
We work with increasing finite setsV m called pre-gaskets approximating the finite Sierpinski gasket located inR N−1 (N ≥ 3). The eigenvalues of the discrete Laplacian onV m under the Dirichlet and Neumann boundary conditions are completely determined using the decimation method due to Rammal.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
J. Kigami, A harmonic calculus on the Sierpinski spaces. Japan J. Appl. Math.,6 (1989), 259–290.
R. Rammal and G. Toulouse, Random walks on fractal structures and percolation clustars. J. Physique Lett.,43 (1982), L13-L22.
R. Rammal, Spectrum of harmonic excitations on fractals. J. Physique,45 (1984), 191–206.
Author information
Authors and Affiliations
Additional information
The author would like to thank Professor M. Fukushima and the referee for the most helpful suggestions.
About this article
Cite this article
Shima, T. On eigenvalue problems for the random walks on the Sierpinski pre-gaskets. Japan J. Indust. Appl. Math. 8, 127–141 (1991). https://doi.org/10.1007/BF03167188
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF03167188