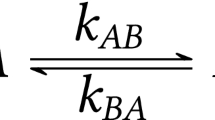Abstract
Variable temperature two-dimensional nuclear Overhauser enhancement experiment (2-D NOESY) is used to extract the rate constants and cross-relaxation rates that contribute to the same cross-peaks in NOESY spectra. Rate constants (k AB) and cross-relaxation rates (R AB) for two-site spin systems are related to the ratio between the cross-peak and diagonal peak integrals (F) by the expression:R AB -k AB = (1/2τ m)ln[(1 -F)/(1 +F)], where τm is the mixing time. As a model, we investigated the exchange processes in a system of dimer calix[4]arenes of C4v symmetrical configuration with guest inclusion (benzene or benzene-d6), where the measurement of exchange processes is hindered by the presence of strong nuclear Overhauser enhancement between protons in adjacent aromatic rings in the cone conformation of the calix[4]arene.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Jackman L.M., Cotton F.A. (eds.): Dynamic Nuclear Magnetic Resonance Spectroscopy, part I, p. 660. New York: Academic Press 1975.
Binsch G.: J. Am. Chem. Soc.91, 1304–1309 (1969); Hofner D., Lesko S.A., Binsch G.: Org. Magn. Reson.11, 179–196 (1978); Aganov A.V., Klochkov V.V., Samitov Yu.Yu.: Usp. Khim.54, 1585-1612 (1985)
Sandström J.: Dynamic NMR Spectroscopy, p. 226. London: Academic Press 1982.
Ernst R.R., Bodenhausen B., Wokaun A.: Principles of Nuclear Magnetic Resonance in One and Two Dimensions, p. 610. Oxford: Oxford University Press 1987.
Van de Ven F.J.M.: Multidimensional NMR in Liquids: Basic Principles and Experimental Methods, p. 399. New York: Wiley-VCH 1995.
Wagner G., Bodenhausen G., Muller N., Rance M., Sorensen O.W., Ernst R.R., Wuthrich K: J. Am. Chem. Soc.107, 6440–6446 (1985)
Desvaux H., Berthault P., Birlirakis N., Goldman M.: J. Magn. Reson. A108, 219–229 (1994); Fejzo J., Westler W.M., Macura S., Markley J.L.: J. Magn. Reson.92, 195–203 (1991)
States D.J., Haberkorn R.A., Ruben D.J.: J. Magn. Reson.48, 286–292 (1982)
Atkins P.W.: Physical Chemistry, p. 995. Oxford: Oxford University Press 1990.
Shimizu K.D., Rebek J. Jr.: Proc. Natl. Acad. Sci. USA92, 12403–12407 (1995); Mogck O., Bohmer V., Vogt V.: Tetrahedron52, 8489–8496 (1996)
Mogck O., Pons M., Bohmer V., Vogt W.: J. Am. Chem. Soc.119, 5706–5712 (1997)
Pons M. (ed.): NMR in Supramolecular Chemistry, p. 337. Dordrecht: Kluwer Academic Publishers 1999.
Oki M.: Application of Dynamic NMR Spectroscopy to Organic Chemistry, p. 423. New York: VCH Publishers 1985.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Klochkov, V.V., Karatayeva, F.K., Shaikhutdinov, R.A. et al. Separation of cross-relaxation and exchange in two-site spin systems without resolved couplings. Appl. Magn. Reson. 22, 431–438 (2002). https://doi.org/10.1007/BF03166123
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF03166123