Skip to main content
SpringerLink
Log in

Nonlinear structural analysis using integrated force method

  • Published:
Sadhana Aims and scope Submit manuscript

Abstract

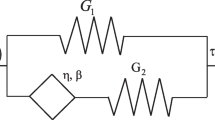
Though the use of the integrated force method for linear investigations is well-recognised, no efforts were made to extend this method to nonlinear structural analysis. This paper presents the attempts to use this method for analysing nonlinear structures. General formulation of nonlinear structural analysis is given. Typically highly nonlinear bench-mark problems are considered. The characteristic matrices of the elements used in these problems are developed and later these structures are analysed. The results of the analysis are compared with the results of the displacement method. It has been demonstrated that the integrated force method is equally viable and efficient as compared to the displacement method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Kaljevic I, Patnaik S N, Hopkins D A 1996a Development of finite elements for two-dimensional structural analysis using integrated force method.Comput. Struct. 59: 691–706

    Article  MATH  Google Scholar 

  • Kaljevic I, Patnaik S N, Hopkins D A 1996b Three-dimensional structural analysis by the integrated force method.Comput. Struct. 58: 869–886

    Article  MATH  Google Scholar 

  • Kaneko I, Lawo H, Thierauf G 1983 On computational procedures for the force method.Int. J. Numer. Methods Eng. 18: 1469–1495

    Article  MathSciNet  Google Scholar 

  • Nagabhushanam J, Patnaik S N 1989 General purpose program to generate compatibility matrix for the integrated force method.AIAA J. 28: 1838–1842

    Article  Google Scholar 

  • Nagabhushanam J, Srinivas C J 1991 Automatic generation of sparse and banded compatibility matrix for the integrated force method.Comput. Mechanics ’91, International Conference on Computing in Engineering Science, Patras, Greece, pp. 20–25

  • Nayak G C 1980 Finite deformations by finite elements.Proceedings of the Symposium on Large Deformations in memory of Prof B Karunes, pp. 413–429

  • Oden J T, Neighbors A 1976 Network-topological formulation of analysis of geometrically and materially non-linear space frames.Proc. 1st Int. Conf. Space Structures (ed.) R M Davis (London: Blackwell Scientific)

    Google Scholar 

  • Patnaik S N 1973 An integrated force method for discrete analysis.Int. J. Numer. Methods Eng. 16: 236–251

    MathSciNet  Google Scholar 

  • Patnaik S N 1986 The variational energy formulation for the integrated force method.AIAA J. 24: 129–137

    Article  MATH  MathSciNet  Google Scholar 

  • Patnaik S N, Yadagiri S 1976 Frequency analysis of structures.Comput. Methods Appl. Mech. Eng. 9: 245–265

    Article  Google Scholar 

  • Patnaik S N, Hopkins D A, Coroneos, R 1996 Structural optimization with approximate sensitivities.Comput. Struct. 58: 407–418

    Article  MATH  Google Scholar 

  • Robinson J, Haggenmacher G W 1971 Some new developments in matrix force analysis. InRecent advances in matrix methods of structural analysis and design (Univ. Alabama) pp. 183–228

  • Surana K S 1983 Geometrically non-linear formulation for two dimensional curved beam elements.Comput. Struct. 17: 105–114

    Article  MATH  Google Scholar 

  • Topou A 1979A contribution to the systematic analysis of finite element structures using the force method (in German). Doctoral dissertation, Essen University, Essen, Germany

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Aerospace Engineering, Indian Institute of Science, 560 012, Bangalore, India

    N R B Krishnam Raju & J Nagabhushanam

Authors
  1. N R B Krishnam Raju
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J Nagabhushanam
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to N R B Krishnam Raju.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Raju, N.R.B.K., Nagabhushanam, J. Nonlinear structural analysis using integrated force method. Sadhana 25, 353–365 (2000). https://doi.org/10.1007/BF03029720

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF03029720

Keywords

Search

Navigation