Abstract
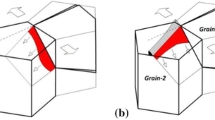
Plastically accommodated creep in an inclusion bearing material (particle- or discontinuous fiber-reinforced metal matrix composite) without any interfacial relaxation mechanisms has been examined. For a material with an elastic-viscoplastic matrix, the non-uniform strain rate in steady state creep is derived using Eshelby’s solution for elastic strain outside an inclusion. The obtained creep strain increment is impotent and does not generate any additional internal stress. During this creep deformation, a dislocation comes in from one direction and goes out in another direction, so that no dislocation nor internal stress but a heterogeneous plastic strain remains in the material. The concrete trajectory of the dislocations climbing over a cylindrical inclusion is calculated and illustrated.
Similar content being viewed by others
References
Z. Hashin,Mechanics of Composite Materials (eds., F. W. Wendt, H. Loebowitz and N. Perrone), p. 201, Pergamon, Oxford (1967).
Y. Li and T. G. Langdon,Mater. Sci. Tech. 15, 357 (1999).
T. Morimoto, T. Yamaoka, H. Lilholt and M. Taya,Trans. ASME 110, 70 (1988).
A. Dlouhy, G. Eggeler and N. Merk,Acta mater. 43, 535 (1995).
K. Tanaka and T. Mori,Acta metall. 18, 931 (1970).
L. M. Brown and W. M. Stobbs,Phil. Mag. 23, 1185 (1971).
R. C. Koeller and R. Raj,Acta metall. mater. 26, 1551 (1978).
T. Mori, T. Okabe and T. Mura,Acta metall. mater. 28, 319 (1980).
D. J. Srolovitz, R. A. P. Luton and M. J. Luton,Phil. Mag. A48, 795 (1983).
A. Kelly and K. N. Street,Proc. Roy. Soc. Lond. A328, 283 (1972).
B. L. Lee and M. E. Mear,J. Mech. Phys. Solids 39, 627 (1991).
T. L. Dragone and W.D. Nix,Acta metall. mater. 38, 1941 (1990).
T. Mori, J. H. Huang and M. Taya,Acta mater. 45, 429 (1997).
E. Sato, T. Ookawara, K. Kuribayashi, and S. Kodama,Acta metall. mater. 46, 4153 (1998).
J. D. Eshelby,Proc. Roy. Soc. A252, 561 (1959).
J. D. Eshelby,Proc. Roy. Soc. A241, 376 (1957).
K. Tanaka and T. Mori,J. Elasticity 2, 199 (1972).
R. Furuhashi and T. Mura,J. Elasticity 9, 263 (1979).
J. F. Nye,Acta metall. 1, 153 (1953).
T. Mura,Proc. IUTAM Symp. Mechanics of Generalized Continua (ed., E. Kroner), p.269, Springer (1968).
Author information
Authors and Affiliations
Additional information
This article is based on a presentation made in the symposium “The 1stKorea-Japan Structural Dynamic Symposium”, held at Sunchon National University, Sunchon, Korea, August 5 ~ 8, 1999 under the auspices of The Korean Institute of Metals and Materials and the Research and Development Center for Automobile Parts and Materials.
Rights and permissions
About this article
Cite this article
Sato, E., Kuribayashi, K. Dislocation movement around an inclusion during plastically-accommodated creep at high temperatures. Metals and Materials 6, 1–5 (2000). https://doi.org/10.1007/BF03026337
Issue Date:
DOI: https://doi.org/10.1007/BF03026337