Some properties of price-consumption curves and income-consumption curves

Summary

The theory of indifference maps is a static theory for consumer’s behaviour. As an illustration of this theory we examine in this note the demand reactions of an individual consumer in three situations. Given the pricesp ₁ …,p _n and his income μ, let Q=(q ₁, …,q _n) be the consumer’s optimal budget. Now in the first place, if one price is allowed to vary, sayp _i, while the income and the other prices are held fixed, the optimal budget will describe a curve known as aprice-consumption curve. Makingi=1, …,n we obtainn such curves passing through Q, say A₁, …, A_n. Second, consider an inflatory situation where all prices vary in proportion, while income μ is constant. In the staic theory of indifference maps this is equivalent to allowing μ to vary while all prices are held fixed. Thus the optimal budget will describe what is known as theincome-consumption curve which passes through Q, say C. Third, suppose in the inflatory situation that one of the prices, say p_i, is held fixed. The optimal budget will then describe a certain curve, say B₁; this will be called aprice-consumption curve of type B. There aren such curves which pass through Q, say B₁, …, B_n.

The price-consumption curves A₁ and B_i and the income-consumption curve C form a convenient geometric representation of the demand functions of the consumer.

The equations of the curves A_i, B_i, C are given in no. 1. Certain simple interrelations between these curves are pointed out in no. 2. In no. 3, finally, we examine the orientation of the curves A_i; anaiogous results are obtained for the curves B_i.

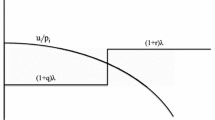
The results of no. 2 are as follows. In the case of two goods,n=2, theprice-consumption curves A₁ and B₂ will coincide, and likewise A₂ and B₁. Considering the passage through Q for falling (rising) prices, the three curves A₁=B₂, A₂=B₁ and C will pass through the budget linep ₁q_r+p₂q₂=μ from below (above). In this passage, C is intermediate between A₁=B₂ and A₂=B₁. In the case ofn goods, all of the2n curves A_i, B_i will in general be different. It is a rather typical situation that a curve A_i will be more or less perpendicular to the corresponding curve B_i. In the passage through Q for falling (rising) prices, the 2n+1 curves A_i, B_i, C will pass through the budget plane σp _iq_i=μ from below (above). On the upper side of the budget plane, the curves A_i will form the edges of a corner at Q, say Λ. Considering the passage of the curve C through the point Q. it is shown that this passage will always take place within the corner Λ. A similar theorem holds for the curves B_i and C.

In no. 3 the geometric interpratation of demand functions is carried further; this leads to a theorem on what is known as the substitution effect. As an immediate corollary, the theorem implies that there is the following similarity between the corner Λ and the corner which the positive coordinate axesq ₁ form at the origin: The consecutive order of the edges A_i at Λ is the same as the order of the axesq _i at the origin; moreover, if we use the direction of the curve C at Q to project the curves A_i into the budget plane, the projection of A_i will form a smaller angle with theq _i-axis than with any other coordinate axes. Again, statements of the same type hold true for the curves B_i. The theorem in question is proved by an intuitive argument. An alternative, purely analytic proof of the theorem, ends the paper.