Abstract
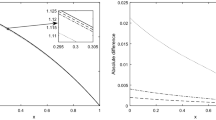
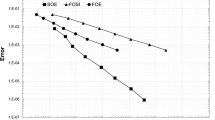
In this note, we present a numerical scheme for finding an approximate solution of an equation which can be viewed as a model for spatial diffusion of age-dependent biological populations. Discretization of the model yields a linear system with a block tridiagonal matrix. Our main concern will be discussion of stability for this scheme by examining the eigenvalues of the block tridiagonal matrix. Numerical results are presented.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
H. Von Foerster,Some remarks on changing populations: The kinetirs of cell proliferation,Grune and stratton, New York, 1959.
M.E. Gurtin, and R.C. MacCamy,Nonlinear age dependent population dynamics, Arch. Rational Mech. Anal.54(1974), 281–300.
M.E. Gurtin,Some questions and open problems in cotinuum mechanics and population dynamics, J. Differential Equations,48(1983), 293–312.
F. Hoppensteadt,Mathematical theories of populations: Demographics, Genetics and Epidemics, Soc. Ind. Appl. Math., Phildelphia, 1975.
R.C. MacCamy,A population model with nonlinear diffusion, J. Differential Equations,39(1981), 52–57.
K.E. Swick, A nonlinear age-dependent model of single species population dynamics, SIAM J. Appl. Math.,32(1977), 484–498.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kerayechian, A. On a certain finite difference scheme for a model for diffusion of biological populations. Korean J. Comput. & Appl. Math. 6, 353–363 (1999). https://doi.org/10.1007/BF03014380
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/BF03014380