Skip to main content
SpringerLink
Log in

A non-Markovian evolution model of HIV population with bunching behaviour

  • Published:
Korean Journal of Computational & Applied Mathematics Aims and scope Submit manuscript

Abstract

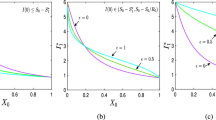
In this paper we propose a model of HIV population through method of phases with non-Markovian evolution of immigration. The analysis leads to an explicit differential equations for the generating functions of the total population size. The detection process of antibodies (against the antigen of virus) is analysed and an explicit expression for the correlation functions are provided. A measure of bunching is also introduced for some particular choice of parameters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Anderson, R.M.,Population dynamics of infectious diseases, Chafman and Hall, London 1982.

    Book  Google Scholar 

  2. Bailey, N.T.J.,The Mathematical theory of infectious diseases, Griffin: London, 1975.

    Google Scholar 

  3. Bailey, N.T.J.,The role of statistics in controlling and eradicating infectious diseases, Statistician 34 (1985), 3–17.

    Article  Google Scholar 

  4. Bailey, N.T.J.,Macro modelling and predcition of epidemic spread at community level, Math Modelling, 7 (1986), 689–717.

    Article  MathSciNet  Google Scholar 

  5. Bartlett, M.S.,Stochastic Processes, 2nd edition (Cambridge University Press, Cambridge) 1966.

    Google Scholar 

  6. Dietz, K. and Schenzle, D.,Mathematical models for infectious disease statistics. In a celebration of statistics (Editors A.C. Atkinson and S.K. Fienberg), Springer, New York (1985), 167–204.

    Chapter  Google Scholar 

  7. Harris, T.E.,Theory of Branching Process (Springer: Berlin) 1963.

    Book  Google Scholar 

  8. Isham, V.,Mathematical modelling of the transmission dynamics of HIV infection and AIDS, a review, JRSS (1987), 5–23.

  9. Kendall, D.G.,Stochastic Processes and Population Growth, J.R. Statistics Society, B-11, pp 230–264, 1949.

    MathSciNet  Google Scholar 

  10. Sridharan, V. and Jayashree P.R.,A Model of HIV population to seropositivity. accepted in Korean J. Comput. and Appl. Math. (in press)

  11. Srinivasan, S.K.,Stochastic point process and their applications, (Griffin: London), 1974.

    Google Scholar 

  12. Srinivasan, S.K.,Point process models of cavity radiation and detection, Charles Griffin and Co. Ltd., 1988.

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Anna University, 600 025, Chennai, India

    V. Sridharan & P. R. Jayashree

Authors
  1. V. Sridharan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. P. R. Jayashree
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. Sridharan.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Sridharan, V., Jayashree, P.R. A non-Markovian evolution model of HIV population with bunching behaviour. Korean J. Comput. & Appl. Math. 5, 695–705 (1998). https://doi.org/10.1007/BF03008892

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF03008892

AMS Mathematics Subject Classification

Key word and phrases

Search

Navigation