Abstract
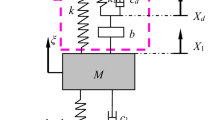
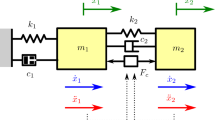
The main objectives of this study are to examine the random responses of a vibration absorber system with autoparametric coupling in the neighborhood of internal resonance subjected to narrow band random excitation by Gaussian closure scheme and to compare the results with those obtained by Monte Carlo simulation. The Monte Carlo simulation is found to support the main features of the nonlinear modal interaction in the neighborhood of internal resonance conditions. The jump phenomenon of the cantilever mode and saturation phenomenon of the main system are shown to occur if the excitation bandwidth is sufficiently small.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Cho, D. S. and Lee. W. K., 2000, “Modal Interactions of a Randomly Excited Hinged-Clamped Beam,”Journal of Sound & Vibration, Vol. 237, No. 3, pp. 377–393.
Haxton, R. S. and Barr, A. D. S., 1972, “The Autoparametric Vibration Absorber,”ASME Journal of Engineering for Industry, Vol. 94, pp. 119–125.
Ibrahim, R. A. and Li, W., 1988, “Structural Modal Interaction with Combination Internal Resonance under Wide-Band Random Excitation, ”Journal of Sound & Vibration, Vol. 123, No. 3, pp. 473–495.
Ibrahim, R. A. and Roberts, J. W., 1976, “Broad Band Random Excitation of a Two-De-gree-of-Freedom System with Autoparametric Coupling,”Journal of Sound & Vibration. Vol. 44, No. 3, pp. 335–348.
Ibrahim, R. A. and Roberts, J. W., 1977, “Stochastic Stability of the Stationary Response of a System with Autoparametric Coupling,”Zeitschrift für Angewandte Mathematik and Mechanik, Vol. 57. pp. 643–649.
Ibrahim, R. A., 1995, “Recent Results in Random Vibrations of Nonlinear Mechanical Systems, ”ASME Journal of Vibration, Acoustics, Stress, and Reliability in Design, Vol. 117, pp. 222–233.
Ibrahim, R. A., 1991, “Nonlinear Random Vibration: Experimental Results,”Applied Mechanics Review, Vol. 44, pp. 423–446.
Lee. W. K. and Cho, D. S, 1998, “Influence of Internal Resonance on Responses of a Spring-Pendulum System under Broad Band Random Excitatiom,”Journal of KSNVE, Vol. 8, No. 3, pp. 399–407.
Lee. W. K. and Cho, D. S., 2000, “Damping Effect of a Randomly Excited Autoparametric System,”Journal of Sound & Vibration, Vol. 236, No. 1, pp. 23–31.
Lee. W. K. and Hsu, C. S., 1994, “A Global Analysis of an Harmonically Excited Spring-Pendulum System with Internal Resonance,”Journal of Sound & Vibration, Vol. 171, No. 3, pp. 335–359.
Li, W. and Ibrahim, R. A., 1990, “Monte Carlo Simulation of Coupled Nonlinear Oscillators under Random Excitations,”ASME Journal of Applied Mechanics, Vol. 57, pp. 1097–1099.
Lin, Y. K. and Cai, G. Q., 1995,Probabilistic Structural Dynamics Advanced Theory and Application, McGraw-Hill, Inc.
Minorsky, N., 1962,Nonlinear Oscillations, Princeton: Roberty E. Krieger.
Nayfeh, A. H. and Mook, D. T., 1979,Nonlinear Oscillation, Wiley-Interscience.
Roberts. J. W.. 1980, “Random Excitation of a Vibratory System with Autoparametric Interaction, “Journal of Sound & Vibration, Vol. 69. No. 1, pp. 101–116.
Shinozuka, M. and Deodatis, G., 1991, “Simulation of Stochastic Processes by Spectral Representation, “Applied Mechanics Review, Vol. 44. pp. 191–204.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Cho, D.S., Mo, C.K., Ban, G.S. et al. Modal interactions in an autoparametric vibration absorber to narrow band random excitation. KSME International Journal 17, 97–104 (2003). https://doi.org/10.1007/BF02984290
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/BF02984290