Abstract
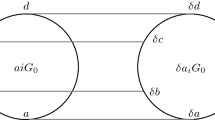
We define a class Γ of 4-regular Cayley graphs on abelian groups and prove every element of Γ to be decomposable into two Hamiltonian cycles. This result is a special case of a conjecture ofB. Alspach and includes a theorem ofJ.-C. Bermond et al. as a subcase.
Similar content being viewed by others
References
B. Alspach. Unsolved problem 4.5.Ann. Discrete Math. 27 (1985), 464.
J.-C. Bermond, O. Favaron andM. Maheo. Hamilton decomposition of Cayley graphs of degree 4.J. Comb. Theory B46 (1989), 142–153.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Baumann, U., Lesch, M. & Schmeichel, I. A note on Hamiltonian decompositions of Cayley graphs. Abh.Math.Semin.Univ.Hambg. 65, 105–111 (1995). https://doi.org/10.1007/BF02953317
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02953317