Differential equation for continuous normalization

Abstract

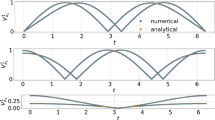
When the response of a dynamical system is seemingly random and is confined in a finite region and shows extreme sensitivity to small changes in initial conditions, we say that the motion is chaotic. To represent chaos of a system precisely and quantitatively, we employ measurement quantity that represents the system's degree of chaos such as a Lyapunov exponent. A way of computing a Lyapunov exponent employs periodic renormalization for the state perturbation vector. However, the application of periodic renormalization for a Lyapunov exponent computation poses difficulties. One difficulty is exponential growth of the norm of the state perturbation vector. A common approach for avoiding this computational problem is periodic renormalization. However, periodic renormalization raises a discontinuity in the state perturbation vector that is not a standard case in optimal control theory as one wants to extremize chaos by manipulating a Lyapunov exponent. To circumvent the exponential growth in magnitude and the state perturbation vector discontinuity problem, one may employ a method of “continuous normalization” which replaces periodic discontinuous renormalization with differential equations that correspond to continuous normalization at each instant of time. This study provides details concerning the development of continuous normalization technique and presents an example for some systems. Also the comparison between the result produced by continuous normalization and that by the periodic renormalization of the state perturbation vector will be given.