Abstract
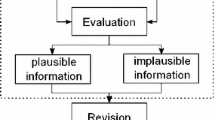
The aim of this paper is to extend the system of belief revision developed by Alchourrón, Gärdenfors and Makinson (AGM) to a more general framework. This extension enables a treatment of revision not only by single sentences but also by any sets of sentences, especially by infinite sets. The extended revision and contraction operators will be called general ones, respectively. A group of postulates for each operator is provided in such a way that it coincides with AGM's in the limit case. A notion of the nice-ordering partition is introduced to characterize the general contraction operation. A computation-oriented approach is provided for belief revision operations.
Similar content being viewed by others
References
Alchourrón C E, Gärdenfors P, Makinson D. On the logic of theory change: Partial meet contraction and revision functions.The Journal of Symbolic Logic, 1985, 50(2): 510–530.
Brewka G. Preferred subtheories: An extended logical framework for default reasoning. InProceedings of IJCAI-89, Detroit, Mich. 1989, pp.1034–1048.
Brewka G. Cumulative default logic: In defense of nonmonotonic inference rules.Artificial Intelligence, 1991, 50: 183–205.
Boutilier C. Revision sequences and nested conditionals. InProceedings of IJCAI-95, pp.519–525, 1993.
Boutilier C. Unifying default reasoning and belief revision in a modal framework.Artificial Intelligence, 1994, 68: 33–85.
Cerro L F, Herzig A, Lang J. From ordering-based nonmonotonic reasoning to conditional logic.Artificial Intelligence, 1994, 66: 375–393.
Dubois D, Prade H. Epistemic entrenchment and possibilistic logic.Artificial Intelligence, 1991, 50: 223–239.
Fuhrmann A. On the modal logic of theory change. InThe Logic of Theory Change (Lecture Notes in Computer Science 465), Fuhrmann A, Morreau M (eds.), Springer-Verlag, 1991, pp.259–281.
Fuhrmann A, Hansson S O. A survey of multiple contractions.Journal of Logic, Language, and Information, 1994, 3: 39–76.
Gärdenfors P. Propositional logic based on the dynamics of belief.The Journal of Symbolic Logic 1985, 50(2): 390–394.
Gärdenfors P. Knowledge in Flux: Modeling the Dynamics of Epistemic States. The MIT Press, 1988.
Gärdenfors P, Makinson D. Nonmonotonic inference based on expectations.Artificial Intelligence, 1994, 65: 197–245.
Hansson S O. A dyadic representation of belief. InBelief Revision Gärdenfors P (ed.), Cambridge University Press, Cambridge, 1992, pp.89–121.
Hansson S O. Theory contraction and base contraction unified.The Journal of Symbolic Logic, 1993, 58(2): 602–625.
Hansson S O. Reversing the Levi identityJournal of Philosophical Logic 1993, 22: 637–669.
Hájek P. Epistemic entrenchment and arithmetical hierarchy.Artificial Intelligence, 1991, 62: 79–87.
Jech T. Set Theory. Academic Press, New York, 1978.
Katsuno H, Mendelzon A O. Propositional knowledge base revision and minimal change.Artificial Intelligence, 1991, 52: 203–294.
Makinson D, Gärdenfors P. Relations between the logic of theory change and nonmonotonic logic. InThe Logic of Theory Change, (Lecture Notes in Computer Science 465), Fuhrmann A, Morreau M (eds.), Springer-Verlag, Berlin, Germany, 1991, pp.185–205.
Nebel B. Reasoning and Revision in Hybrid Representation System (Lecture Notes in Artificial Intelligence 422). Springer-Verlag, 1990.
Nebel B. Syntax based approaches to belief revision. InBelief Revision, Gärdenfors P (ed.), Cambridge University Press, Cambridge, 1992, 52–88.
Niederèe R. Multiple contraction: A further case against Gärdenfors' principle of recovery. InThe Logic of Theory Change (Lecture Notes in Computer Science 465), Fuhrmann A, Morreau M (eds.), Springer-Verlag, 1991, pp.322–334.
Rott H. On the logic of theory change: More maps between different kinds of contraction function. InBelief Revision, Gärdenfors P (ed.), Cambridge University Press, Cambridge, 1992, pp. 122–140.
Rott H. Belief contraction in the context of the general theory of rational choice.The Journal of Symbolic Logic, 1993, 58(4): 1426–1450.
Weydert E. Relevance and revision: About generalizing syntax-based belief revision. InEuropean Workshop JELIA'92 (Lecture Notes in Artificial Intelligence 633), Pearce D, Wagner G (eds.), Springer-Verlag, Berlin, 1992, pp. 126–138.
Zhang Dongmo. A general framework for belief revision. InProc. of 4th Int'l Conf. for Young Computer Scientists, Peking University Press, 1995, 574–581.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was partly supported by the High-Tech R/D Program of China.
Zhang Dongmo received a Diploma in mathematics from Nanjing Normal University in 1980 and his M.S. degree in computer application from Nanjing University of Aeronautics and Astronautics (NUAA) in 1992. He has been on the faculty of the Department of Computer Science at NUAA since 1993 and is a Ph.D. candidate at Institute of Computer Science at NUAA. His research interets include mathematical logic, automated reasoning, knowledge representation and reasoning and distributed artificial intelligence.
Rights and permissions
About this article
Cite this article
Zhang, D. Belief revision by sets of sentences. J. of Comput. Sci. & Technol. 11, 108–125 (1996). https://doi.org/10.1007/BF02943527
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02943527