Abstract
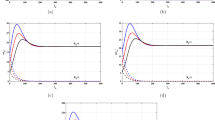
A population model of infected T-4 cell is modeled as a point process using method of phases with special types of time-dependencies. The duration of these phases are themselves independent and exponentially distributed random variables. The analysis leads to an explicit differential equations for the generating functions of the infected T-4 cells from which the first and second order moments are calculated. Graphs are drawn for the expected number of infected T-4 cells. Finally interpretation of results are given. The detection process is explicitly introduced and its characteristics are obtained. Also for different parametric values the stationarity distribution are tabulated.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Alan S. Perelson, Krischer D. E. Boer R. D.,Dynamics of HIV infection of CD4 + T cells, Mathematical Biosciences114 (1993), 81–125.
Isham V.,Mathematical Modeling of the Transmission Dynamics of HIV infection on AIDS: a review, J Roy Statist Soc. (1987), 5–25. itemJones M. E. and Solomon P. J.,A note on the concept of the incubation period in HIV infection, J Roy Statist Soc. Ser. A151 (1988), 40–42.
Nagarjuna N. S. and Iyer K. S. S.,Modeling growth of HIV to seropositivity, Proceedings of ICSOS (1994), 137–143.
Kelly P. C. and Kleiner W. H.,Theory of electromagnetic field measurement and photoelectron counting, Phys. Rev.136 (1964), 316–334.
Shepherd T. J.,A model for photo detection of single-mode cavity radiation, Opt. Act.28 (1981), 567–583.
Srinivasan S. K., Pramana J. Phys.27 (1989), 19–31.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Sridharan, V., Jayashree, P.R. A population model of infected T-4 cells in aids. Korean J. Comput. & Appl. Math. 6, 99–110 (1999). https://doi.org/10.1007/BF02941910
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/BF02941910