Abstract
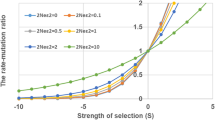
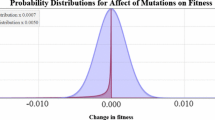
We have used diffusion and branching process methods to investigate fixation rates, probabilities of survival per generation, and times to fixation of mutant genes under different selection methods incorporating individual and family information. Diffusion approximations fit well to simulated results even for large selection coefficients. Methods that give much weight to family information, such as BLUP evaluation which is widely used in animal breeding, reduce fixation rates of mutant genes because of the reduced effective population sizes. In general, it is observed that even mutants with relatively small heterozygous effects (say 0.1 phenotypic standard deviation) are practically ‘safe’ (i.e. their probability of loss from one generation to the next is smaller than, say, 10%) after just a few generations, typically less than 10. For methods of selection with larger effective size, such as within-family selection, the mutant is ‘safe’ in the population somewhat earlier but eventual fixation takes a longer time. Finally we evaluate the amount by which the use of marker assisted selection reduces the fixation probability of newly arisen mutants.
Similar content being viewed by others
References
Bulmer M. G. 1980The mathematical theory of quantitative genetics (Oxford: Clarendon Press)
Caballero A., Santiago E. and Toro M. A. 1996 Systems of mating to reduce inbreeding in selected populations.Anim. Sci. 62: 431–442
Ewens W. J. 1963 Numerical results and diffusion approximations in a genetic process.Biometrika 50: 241–250
Falconer D. S. and Mackay T. F. C. 1996Introduction to quantitative genetics, 4th edn. (Harlow, UK: Longman)
Gale J. S. 1990Theoretical population genetics (London: Unwin Hyman) ch. 4
Grundy B., Caballero A., Santiago E. and Hill W. G. 1994 A note on using biased parameter values and non-random mating to reduce rates of inbreeding in selection programmes.Anim. Prod. 59: 465–468
Henderson C. R. 1984Application of linear models in animal breeding. University of Guelph, Canada Hill W. G. 1969 On the theory of artificial selection in finite populations.Genet. Res. 13: 143–163
Hill W. G. 1976 Order statistics of correlated variables and implications in genetic selection programmes.Biometrics 32: 889–902
Hill W. G. 1982 Predictions of response to artificial selection from new mutations.Genet. Res. 40: 255–278
Hill W. G. 1985 Fixation probabilities of mutant genes with artificial selection.Genet. Sel. Evol. 17: 351–358
Hill W. G., Caballero A. and Dempfle L. 1996 Prediction of response to selection within families.Genet. Sel Evol. (in press)
Kimura M. 1957 Some problems of stochastic processes in genetics.Ann. Math. Stat. 28: 882–901
Kimura M. 1962 On the probability of fixation of mutant genes in a population.Genetics 47: 713–719
Kimura M. 1964 Diffusion models in population genetics.J. Appl. Prob. 1: 177–232
Kimura M. and Ohta T. 1969 The average number of generations until fixation of a mutant gene in a finite population.Genetics 61: 763–771
Lande R. and Thompson R. 1990 Efficiency of Marker-Assisted-Selection in the improvement of quantitative traits.Genetics 124: 743–756
Latter B. D. H. 1965 The response to artificial selection due to autosomal genes of large effect. I. Changes in gene frequency at an additive locus.Aust. J. Biol. Sci. 18: 585–598
Lush J. L. 1947 Family merit and individual merit as bases for selection.Am. Nat. 81: 241–261, 362-379
Lynch M. 1988 The rate of polygenic mutation.Genet. Res. 51: 137–148
Robertson A. 1960 A theory of limits in artificial selection.Proc. R. Soc. London B153: 234–249
Robertson A. 1961 Inbreeding in artificially selected programmes.Genet. Res. 2: 189–194
Santiago E. and Caballero A. 1995 Effective size of populations under selection.Genetics 139: 1013–1030
Verrier E., Colleau J. J. and Foulley J. L. 1993 Long term effects of selection based on animal model BLUP in a finite population.Theoret. Appl. Genet. 87: 446–454
Villanueva B., Woolliams J. A. and Simm G. 1994 Strategies for controlling rates of inbreeding in MOET nucleus schemes for beef cattle.Genet. Sel. Evol. 26: 517–535
Wei M., Caballero A. and Hill W. G. 1996 Selection response in finite population.Genetics (in press)
Woolliams J. A., Wray N. R. and Thompson R. 1993 Prediction of long-term contributions and inbreeding in populations undergoing mass selection.Genet. Res. 62: 231–242
Wray N.R. and Hill W G 1989 a syptonic rates of response from index selection.Anim.Prod. 49: 217–227
Wray N.R. and Thompson R. 1990 Prediction of rates of inbreeding in selected population.Genet.Res. 55: 41–54
Wray N. R., Woolliams J. A. and Thompson R. 1994 Predicition of rates of inbreeding in population undergoing index selection.Theoret.Appl.Genet. 87: 878–892
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Caballero, A., Wei, M. & Hill, W.G. Survival rates of mutant genes under artificial selection using individual and family information. J. Genet. 75, 63–80 (1996). https://doi.org/10.1007/BF02931752
Issue Date:
DOI: https://doi.org/10.1007/BF02931752