Skip to main content
SpringerLink
Log in

A 1D lattice-Boltzmann model with energy equation

  • Part II. Invited Lectures and Contributed Lectures
  • 3. Non-Numerical Parallel Algorithms
  • Published:
Wuhan University Journal of Natural Sciences

Abstract

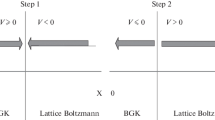
In this paper, a 1D lattice-Boltzmann model with energy equation for simulating gas dynamics is studied. The model is applied to simulating the famous shockwave tube problem, which shows good agreement of the numerical results with those of theoretical analysis and other numerical methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Alexander, F. J., Chen, H., Chen, S., and Doolen G. D. (1992): Lattice Boltzmann model for compressible fluids.Phys. Rev. A,46.1967–1970.

    Article  Google Scholar 

  2. Qian, Y. H., d'Humieres, D. and Lallemand, P. (1992): Lattice BGK models for Navier-Stokes equation.Europhys. Lett.,17, 479–484.

    Article  MATH  Google Scholar 

  3. Ponce Dawson, S., Chen, S., and Doolen, G. D. (1993): Lattice Boltzmann computations for reaction-diffusion equations.J. Chem. Phys.,98,1514–1522.

    Article  Google Scholar 

  4. Li Yuanxiang, Kang Lishan and Wu Zhijian, A new class of lattice gas methods (1993).Neural Parallel & Scientific Computations,1,43.

    MATH  MathSciNet  Google Scholar 

  5. Chen, S., Chen H., Martinez D. and Matthaeus W. H. (1991): Lattice Boltzmann model for simulation of magneto-hydrodynamics.Phys. Rev. Lett.,67, 3776.

    Article  Google Scholar 

  6. Jin Baoxia (1994): On an essentially conservative scheme for hyperbolic conservation laws.J. Comp. Phys.,112,308–315.

    Article  MATH  Google Scholar 

  7. Zou Xiufen, Chen Juhua and Li Yuanxiang (1994): Overlapping lattice Boltzmann models,Foundation of Intelligent Computers'94, Tsinghua University Press. (in Chinese), 71–77.

  8. Sod, G.A. (1978): A Survey of Several Finite Difference Methods for Systems of Non-Linear Hyperbolic Conservation Laws.J. Comp. Phys.,27, 1.

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Wuhan University of Hydraulic and Electric Engineering, 430072, Wuhan, P.R. China

    Zou Xiufen

  2. State Key Laboratory of Software Engineering, Wuhan University, 430072, Wuhan, P.R. China

    Li Yuanxiang

  3. Department of Mathematics, Shantou University, 515063, Shanton Guangdong, P.R. China

    Nie Sixiang

Authors
  1. Zou Xiufen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Li Yuanxiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Nie Sixiang
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

This work was supported in part by Chengguang Project of Wuhan City. Open Foundation of Laboratory of Computational Physics, Beijing

Rights and permissions

Reprints and permissions

About this article

Cite this article

Xiufen, Z., Yuanxiang, L. & Sixiang, N. A 1D lattice-Boltzmann model with energy equation. Wuhan Univ. J. of Nat. Sci. 1, 478–482 (1996). https://doi.org/10.1007/BF02900874

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02900874

Keywords

Search

Navigation