Abstract
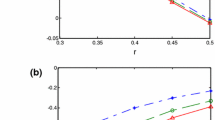
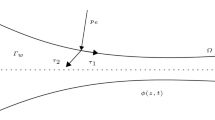
The fractional calculus approach in the constitutive relationship model of second-order fluid is introduced and the flow characteristics of the viscoelastic fluid in double cylinder rheometer are studied. First, the analytical solution of which the derivative order is 1/2 is derived with the analytical solution and the reliability of Laplace numerical inversion based on Crump algorithm for the problem is verified, then the characteristics of second-order fluid flow in the rheometer by using Crump method is analyzed. The results indicate that the more obvious the viscoelastic properties of fluid are, the more sensitive the dependence of velocity and stress on fractional derivative order is.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Liu Ciqun, Huang Junqi, Analytical solution for equations of unsteady flow fo non-Newtonian fluids in tube,Applied Mathematics and Mechanics (in Chinese), 1989, 10(11).
Yan Zongyi, Wang Huiming, Zhuang Fengyuan. Inertial effection of Maxwell fluid in double cylinder rheometer, inThe 4 th National Conference on Multiphase, Non-Newtonian and Physiochemical Fluids Mechanics (in Chinese), Xi’an: Petroleum College Press, 1993.
Slonimsky, G. L., Laws of mechanical relaxation processes in polymers,J. Polym. Sci. C, 1967, (16): 1667.
Bagly, R. L., A theoretical basis for the application of fractional,calculus to viscoelasticity,J. of Rheology, 1983, 27(3): 201.
Rogers, L., Operators and fractional derivatives for viscoelastic constitutive equations,J. of Rheology, 1983, 27(4): 351.
Friedrich, C., Relaxation and retardation function of the Maxwell model with fractional derivatives,Rheology Acta, 1991, 30: 151.
Li Jian, Jiang Tiqian, The research on viscoelastic constitutive relationship model with factional derivative operator, inThe National Rheological Conference (in Chinese), Guangzhou: South China Technological University Press, 1993.
Crump, K. S., Numerical inversion of Laplace transfrom using a Fourier series approximation,J. Assoc.Comput.Mach., 1976, 23(1): 89.
He Guangyu, The application of new numerical inversion method of Laplace transform in analyzing vertical fracture flow, inProceedings of International Petroleum and Petrochemical Techniques Conference (in Chinese), Beijing: Petroleum Industrial Press, 1994, 7.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Huang, J., He, G. & Liu, C. Analysis of general second-order fluid flow in double cylinder rheometer. Sci. China Ser. A-Math. 40, 183–190 (1997). https://doi.org/10.1007/BF02874437
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02874437