Abstract
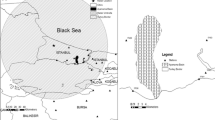
Quantitative precipitation forecasting (QPF) has been attempted over the Narmada Catchment following a statistical approach. The catchment has been divided into five sub-regions for the development of QPF models with a maximum lead-time of 24 hours. For this purpose the data of daily rainfall from 56 raingauge stations, twice daily observations on different surface meteorological parameters from 28 meteorological observatories and upper air data from 11 aerological stations for the nine monsoon seasons of 1972–1980 have been utilized. The horizontal divergence, relative vorticity, vertical velocity and moisture divergence are computed using the kinematic method at different pressure levels and used as independent variables along with the rainfall and surface meteorological parameters. Multiple linear regression equations have been developed using the stepwise procedure separately with actual and square root and log-transformed rainfall using 8-year data (1972–1979). When these equations were verified with an independent data for the monsoon season of 1980, it was found that the transformed rainfall equations fared much better compared to the actual rainfall equations. The performance of the forecasts of QPF model compared to the climatological and persistence forecasts has been assessed by computing the verification scores using the forecasts for the monsoon season of 1980.
Similar content being viewed by others
References
Bedekar V C and Banerjee A K 1969 A study of climatological and other rainfall patterns over central India;Indian J. Meteorol. Geophys. 20 23
Bellocq A 1980 Operational models and quantitative precipitation forecasts for hydrological purposes and possibilities of an inter comparison;World Meteorological Organization Geneva, Switzerland
Chien H and Smith P J 1973 On the estimation of kinematic parameters in the atmosphere from radiosonde wind data;Mon Weather Rev. 101 252–261
Doria R S 1990 Environmental impact of Narmada Sagar Project, (New Delhi: Ashish Publishing House), pp 204
Georgakakos K P and Hudlow M D 1983 Quantitative precipitation forecast techniques for use in hydrological forecasting;Bull. Am Meteorol. Soc. 65 1186–1200
Glahn H R and Lowry D A 1972 The use of Model Output Statistics (MOS) in objective weather forecasting;J. Appl. Meteorol. 11 1203–1211
Gupta G R, Srivastava K K, Mehra H C and Bansal S R 1979 Quantitative precipitation forecasting for hydrological prediction over catchment areas with inadequate aerological data by the method of atmospheric water balance;Mausam 30 113–118
India Meteorological Department 1970 Rainfall and variability: Narmada basin,IMD, New Delhi
Jennrich R I 1977 Stepwise regression; statistical methods for digital computers (eds) K Ensleing, A Relston and H S Wilf (New York: John Wiley) pp 58–75
Krishnamurti T N 1986 Work book on numerical weather prediction for the tropics for the training of Class I and Class II meteorological personnelWMO No. 669 WMO, 33–44.
Lowry D A and Glahn H R 1976 An operational model for forecasting probability of precipitation-PEATMOS POP;Mon. Weather Rev. 104 221–232
Mills G A, Tapp R G, McNamara G F and Pike D J 1986 A generalised Australian model output statistics system;Aust. Meteorol. Mag. 34 57–63
O’Brien J J 1970 Alternative solution to the classical vertical velocity problemJ. Appl. Meteorol. 9 197–203
Pant P S, Abbi S D S and Gupta D K 1969 A hydrometeorological study of the heavy floods in Narmada and Tapti; Flood control and the use of river water resources symposium held at South Gujarat University, Surat (Surat, South Gujarat University) p 151
Perrone T J and Miller R G 1985 Generalised exponential markov and model output statistics; A comparative verification;Mon. Weather Rev. 113 1524–1541
Raghavan K 1973 Break-monsoon over India;Mon. Weather Rev. 101 33
Sen P N 1991 A mathematical model for flood forecasting purposes;Mausam 42 201–204
Singh N, Soman M K and Krishna Kumar K 1988 Hydroclimatic fluctuations of the upper Narmada Catchment and its association with break-monsoon days over India;Proc. Indian Acad. Sci (Earth Planet. Sci.) 97 87–105
Smithsonian Meteorological Tables (Sixth Edition) 1949 p 350.
Tapp R G and McNamara G F 1989 Experiments using model output statistics to predict precipitation at a tropical location;Aust. Meteorol. Mag. 37 129–139
Upadhyay D S, Apte N Y, Surinder Kaur and Singh S P 1986 A dynamical approach to quantitative precipitation forecast;Mausam 37 369–372
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Kumar, K.K., Soman, M.K. Quantitative precipitation forecasting over Narmada Catchment. Proc. Indian Acad. Sci. (Earth Planet Sci.) 102, 313–328 (1993). https://doi.org/10.1007/BF02861506
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02861506