Abstract
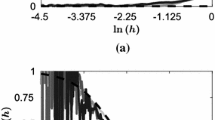
The space overlap of an attractor reconstructed from a time series with a similarly reconstructed attractor from a random series is shown to be a sensitive measure of determinism. Results for the time series for Henon, Lorenz and Rössler systems as well as a linear stochastic signal and an experimental ECG signal are reported. The overlap increases with increasing levels of added noise, as shown in the case of Henon attractor. Further, the overlap is shown to decrease as noise is reduced in the case of the ECG signal when subjected to singular value decomposition. The scaling behaviour of the overlap with bin size affords a reliable estimate of the fractal dimension of the attractor even with limited data.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
F Takens, inDynamical Systems and Turbulence of ‘Springer Lecture Notes in Mathematics’ edited by D A Rand and L-S Young (Springer-Verlag, New York, 1981) vol. 898, p. 366
J-P Eckmann and D Ruelle,Rev. Mod. Phys. 57, 617 (1985)
A Wolf, J B Swift, H L Swinney and J A Vastano,Physica D16, 285 (1985)
D T Kaplan and L Glass,Phys. Rev. Lett. 68, 427 (1972)
D T Kaplan and L Glass,Physica D64, 431 (1993)
L W Salvino and R Cawley,Phys. Rev. Lett. 73, 1091 (1994)
D H Holton and R M May, inThe nature of Chaos edited by T Mullin (Clarendon Press, Oxford, 1993) p. 149
P Grassberger and I Procaccia,Phys. Rev. Lett. 50, 346 (1983)
P Grassberger and I Procaccia,Phys. Rev. A28, 2591 (1983)
E J Kostelich and T Schreiber,Phys. Rev. E48, 1752 (1993)
T Schreiber,Phys. Rev. E48, R13 (1993)
However, a recent report shows that for IID Gaussian noise, correlation dimension can be reliably estimated up to noise levels of 20%. See C DiksPhys. Rev. E53, R4263 (1996)
S H Strogatz,Nonlinear dynamics and chaos (Addison-Wesley Publishing Co., Reading, 1994)
A Provenzale, L A Smith, R Vio and G Murante,Physica D58, 31 (1992)
W H Press, S A Teukolsky, W T Vetterling and B P Flannery,Numerical recipes in Fortran (Cambridge University Press, 1992) p. 295
H Kantz,Phys. Rev. E49, 5091 (1994)
D Broomhead and G P King,Physica D20, 217 (1986)
P Grassberger and I Procaccia,Physica D9, 189 (1983)
J Theiler, A Longlin, B Galdrikin and J D Farmer,Physica D58, 77 (1992)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Gopinathan, M.S. Detection of determinism and randomness in time series: A method based on phase space overlap of attractors. Pramana - J Phys 49, 581–590 (1997). https://doi.org/10.1007/BF02848331
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02848331