Abstract
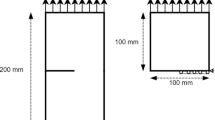
Tensile cracking and subsequent failure of a notched concrete in uniaxial tension is considered to investigate the strain softening behavior of a brittle material. A homogenization technique together with a velocity discontinuity is employed to prevent mesh sensitive behavior of the strain softening material and, using these, a three-dimensional constitutive model involving tensile cracks is derived. It is shown that the thickness of the tensile crack is efficiently removed and, therefore, the stiffness or the softening modulus of the concrete becomes independent of the mesh size. A numerical example in the space of one-, two- and three dimensions is introduced to verify the proposed model and it is found that the softening regime of the cracked concrete is successfully modelled with the proposed homogenized crack element. Future studies will be concentrated on the interlocking crack model and, therefore, a more realistic analysis can be foreseen.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Alfaiate, J., Pires, E. B. and Martins, J. A. C. (1997), “A finite element analysis of non-prescribed crack propagation in concrete”,Comp. & Struct., Vol. 63, pp. 17–26.
Bićanić, N. and Pearce, C. J. (1996), “Computational aspects of a softening plasticity model for plain concrete”,Mech. Coh.-Frict. Mat., Vol. 1, pp. 75–94.
Bodè, L., Tailhan, J. L., Pijaudier-Cobot, G., La Borderie, C. and Clment, J. L. (1997), “Failure analysis of initially cracked concrete structures”,J. Eng. Mech., ASCE, Vol. 123, pp. 1153–1160.
Carol, I., Prat, P. C. and López, C. M. (1997), “Normal/shear cracking model: Application to discrete crack analysis”,J. Eng. Mech., ASCE, Vol. 123, pp. 765–773.
de Borst, R. (1997), “Some recent developments in computational modelling of concrete fracture”,I. J. Frac., Vol. 86, pp. 5–36.
Gopalaratnam, V. G. and Shah, S. P. (1985), “Softening response of plain concrete in direct tension”,ACI J., pp. 310–323.
Hill, R. (1963), “Elastic properties of reinforced solids: some theoretical principles”,J. Mech. Phys. Solids., Vol. 11, pp. 357–372.
Larsson, R. and Runesson, K. (1996), “Element-embedded localization band based on regularized displacement discontinuity”,J. Eng. Mech., ASCE, Vol. 122, pp. 402–411.
Lee, J. S., Pande, G. N., Middleton, J. and Kralj, B. (1996), “Numerical modelling of brick masonry panels subject to lateral loadings”,Comp. & Struct., Vol. 61, pp. 735–745.
Lee, J. S. and Pande, G. N. (1997), “Application of homogenisation technique to a one-dimensional bar exhibiting strain-softening behaviour”,Mat. & Struct., Vol. 30, pp. 506–510.
Nagtegaal, J. C., Parks, D. M. and Rice, J. R. (1974), “On numerically accurate finite element solutions in the fully plastic range”,Comp. Meth. Appl. Mech. Eng., Vol. 4, pp. 153–177.
Nilsson, C. (1997), “Nonlocal strain softening bar revisited”,I. J. Solids & Struct., Vol. 34, pp. 4399–4419.
Ohlsson, U. and Olofsson, T. (1997), “Mixedmode fracture and anchor bolts in concrete analysis with inner softening bands”,J. Eng. Mech., ASCE, Vol. 123, pp. 1027–1033.
Oliver, J. (1989), “A consistent characteristic length for smeared crack models”,I. J. Num. Meth. Eng., Vol. 28, pp. 461–474.
Petrangeli, M. and O bolt, J. (1996), “Smeared crack approaches-material modeling”,J. Eng. Mech., ASCE, Vol. 122, pp. 545–554.
Shah, S. P., Swartz, S. E. and Ouyang, C. (1995),Fracture Mechanics of Concrete, John Wiley & Sons.
Yamaguchi, E. and Chen, W-F. (1990), “Cracking model for finite element analysis of concrete materials”,J. Eng. Mech., ASCE, Vol. 116, pp. 1242–1260.
Additional information
The manuscript for this paper was submitted for review on April 27, 1998.
Rights and permissions
About this article
Cite this article
Lee, J.S., Choi, IY., Bang, Cs. et al. Three-dimensional homogenized crack model for tensile fracture of concrete. KSCE J Civ Eng 3, 37–46 (1999). https://doi.org/10.1007/BF02830734
Issue Date:
DOI: https://doi.org/10.1007/BF02830734