Design of piezocomposite materials and piezoelectric transducers using topology optimization— Part III

Summary

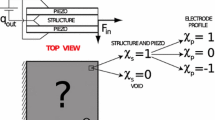
Following the topic introduced in [1, 2] this paper discusses the design of piezoelectric transducers used in applications such as acoustic wave generation and resonators. These applications require goals in the transducer design such as high electromechanical energy conversion for a certain transducer vibration mode and narrowband or broadband response. The development of these devices has been based on the use of simple analytical models, test of prototypes, and analysis by the finite element method. However, in all cases the design is limited to a parametric optimization where only some dimensions of a chosen transducer configuration are optimized. By changing the topology of these devices or their components, we may obtain devices with better performance since the design space of solutions is enlarged. Based on this idea, we have proposed the use of topology optimization for designing these devices. This method consists of finding the distribution of the material and void phases in the design domain that optimizes a defined objective function. The optimized solution is obtained using Sequential Linear Programming (SLP). Considering acoustic wave generation and resonator applications, three kinds of objective functions were defined: maximize the energy conversion for a specific mode or a set of modes; design a transducer with specified frequencies; and design a transducer with narrowband or broadband response. Although only two-dimensional plane strain transducer topologies have been considered in order to illustrate the implementation of the method, it can be extended to three-dimensional topologies. Transducer designs were obtained that conform to the desired design requirements and have better performance characteristics than other common designs.