Abstract
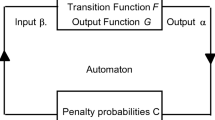
We consider stochastic automata models of learning systems in this article. Such learning automata select the best action out of a finite number of actions by repeated interaction with the unknown random environment in which they operate. The selection of an action at each instant is done on the basis of a probability distribution which is updated according to a learning algorithm. Convergence theorems for the learning algorithms are available. Moreover the automata can be arranged in the form of teams and hierarchies to handle complex learning problems such as pattern recognition. These interconnections of learning automata could be regarded as artificial neural networks.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Banerjee S 1989On stochastic relaxation paradigms for computational vision, PhD thesis, Electrical Engineering Department, Indian Institute of Science, Bangalore
Bush R R, Mosteller F 1958Stochastic models for learning (New York: John Wiley and Sons)
Lakshmivarahan S 1981Learning algorithms — theory and applications (New York: Springer Verlag)
Lakshmivarahan S, Thathachar M A L 1973 Absolutely expedient learning algorithms for stochastic automata.IEEE Trans. Syst., Man Cybern. SMC-3: 281–283
Mason L G, Gu X D 1986 Learning automata models for adaptive flow control in packet-switching networks. InAdaptive and learning systems (ed.) K S Narendra (New York: Plenum)
Mukhopadhyay S, Thathachar M A L 1989 Associative learning of Boolean functions.IEEE Trans. Syst. Man Cybern. SMC-19: 1008–1015
Narendra K S, Mars P 1983 The use of learning algorithms in telephone traffic routing — A methodology,Automatica 19: 495–502
Narendra K S, Thathachar M A L 1989Learning automata — an introduction (Englewood Cliffs,NJ: Prentice Hall)
Ramakrishnan K R 1982Hierarchical systems and cooperative games of learning automata, PhD thesis, Indian Inst. Sci. Bangalore
Sastry P S, Banerjee S, Ramakrishnan K R 1988 A local cooperative processing model for low level vision.Indo-US Workshop on Systems and Signal Processing (ed.) N Viswanadham (New Delhi: Oxford & IBH)
Shapiro I J, Narendra K S 1969 Use of stochastic automata for parameter self-optimization with multimodal performance criteria.IEEE Trans. Syst. Sci. Cybern. SSC-5: 352–360
Thathachar M A L, Sastry P S 1985 A new approach to the design of reinforcement schemes for learning automata.IEEE Trans. Syst., Man Cybern. SMC-15: 168–175
Thathachar M A L, Sastry P S 1986 Relaxation labeling with learning automata.IEEE Trans. Pattern Anal. Mach. Intell. PAMI-8: 256–268
Thathachar M A L, Sastry P S 1987 Learning optimal discriminant functions through a cooperative game of automata.IEEE Trans. Syst., Man Cybern. SMC-17: 73–85
Tsetlin M L 1973Automaton theory and modeling of biological systems (New York: Academic Press)
Williams R J 1988 Toward a theory of reinforcement — learning connectionist systems, Technical Report, NU-CCS-88-3, College of Computer Science, Northeastern University, Boston, MA
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Thathachar, M.A.L. Stochastic automata and learning systems. Sadhana 15, 263–281 (1990). https://doi.org/10.1007/BF02811325
Issue Date:
DOI: https://doi.org/10.1007/BF02811325