Skip to main content
SpringerLink
Log in

Compact surfaces as configuration spaces of mechanical linkages

  • Published:
Israel Journal of Mathematics Aims and scope Submit manuscript

Abstract

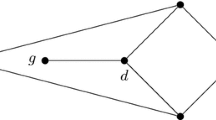
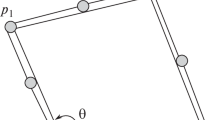
There exists a homeomorphism between any compact orientable closed surface and the configuration space of an appropriate mechanical linkage defined by a weighted graph embedded in the Euclidean plane.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. J. Bochnak, M. Coste and M.-F. Roy,Géométrie algébrique réelle, Springer-Verlag, Berlin, 1987.

    MATH  Google Scholar 

  2. J. Grosjean,Kinematics and Dynamics of Mechanisms. McGraw-Hill, London, 1991.

    Google Scholar 

  3. J.-C. Hausmann,Sur la topologie des bras articulés, Lecture Notes in Mathematics1474, Springer-Verlag, Berlin, 1989, pp. 146–159.

    Google Scholar 

  4. J.-C. Hausmann and A. Knutson,Polygon spaces and Grassmannians, L'Enseignement Mathématique (2)43 (1997), 173–198.

    MATH  MathSciNet  Google Scholar 

  5. B. Jaggi,Punktmengen mit vorgeschriebenen Distanzen und ihre Konfigurationsräume, Inauguraldissertation, Universität Bern, 1992.

  6. D. Jordan,Konfigurationsräume von Gelenkmechanismen, Diplomarbeit, Universität Bern, 1997.

  7. D. Jordan and M. Steiner,Configuration spaces of mechanical linkages, Journal of Discrete and Computational Geometry22 (1999), 297–315.

    Article  MATH  MathSciNet  Google Scholar 

  8. M. Kapovich and J. Millson,On the moduli space of polygons in the Euclidean plane, Journal of Differential Geometry42 (1995), 133–164.

    MATH  MathSciNet  Google Scholar 

  9. M. Kapovich and J. Millson,Universality theorems for configuration spaces of planar linkages, preprint, 1998.

  10. M. Steiner,Realisierungsräume von gewichteten Graphen, Diplomarbeit, Universität Bern, 1997.

  11. A. Wenger,Etudes des espaces de configurations de certains systèmes articulés, Travail de diplôme, Université de Genève, 1988.

Download references

Author information

Authors and Affiliations

  1. Mathematisches Institut der Universität Bern, CH-3012, Bern, Switzerland

    Denis Jordan

  2. Départment de Mathématiques EPF Lausanne, CH-1015, Lausanne, Switzerland

    Marcel Steiner

Authors
  1. Denis Jordan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Marcel Steiner
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Denis Jordan.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Jordan, D., Steiner, M. Compact surfaces as configuration spaces of mechanical linkages. Isr. J. Math. 122, 175–187 (2001). https://doi.org/10.1007/BF02809898

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02809898

Keywords

Search

Navigation