Stochastic claims inflation in IBNR

Summary

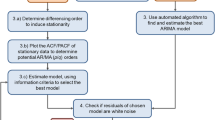
This paper deals with loss reserving under inclusion of stochastic claims inflation, a topic that is of current interest. Note that recently a new paper on it was presented at the international Astin colloquium at Cairns. In the present article it is basically assumed that the discounted claims increase follows an autoregressive model of ARCH-type and that the stochastic yearly interest intensity follows a classical autoregressive model. A procedure to estimate adequately the stochastic discounting factors is deduced. This is combined with the link-ratio technique and the classical forecasting procedure for autoregressive processes, giving a new stochastic loss reserving technique. The whole method is perfect and handy. Its practicability is demonstrated in an example.

Zusammenfassung

Die Arbeit befa\t sich mit der Schadenreservierung unter Einschlu\ der stochastischen Schadeninflation, ein Bereich von momentanem Interesse. Man beachte, da\ kürzlich eine neue Arbeit dazu auf dem internationalen ASTIN Kolloquium in Cairns prÄsentiert wurde. In der vorliegenden Arbeit wird grundlegend angenommen, da\ die diskontierten Schadensteigerungen einem autoregressiven Modell des ARCH-Typs und die jÄhrlichen, stochastischen Inflations-IntensitÄten einem klassischen autoregressiven Modell folgen. Eine Prozedur zur adÄquaten SchÄtzung der stochastischen Diskontierungsfaktoren wird hergeleitet. Diese wird kombiniert mit der Link-Ratio-Technik und der klassischen Vorhersage-Prozedur für autoregressive Prozesse, was insgesamt eine neue stochastische Schadenreservierungstechnik ergibt. Die gesamte Methode ist perfekt und handlich. Ihre PraktikabilitÄt wird an einem Beispiel demonstriert.