Skip to main content
SpringerLink
Log in

Power spectrum estimation of complex signals and its application to Wigner-Ville distribution: A group delay approach

  • Recent Results In Signal Processing And Communications
  • Published:
Sadhana Aims and scope Submit manuscript

Abstract

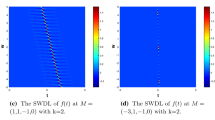
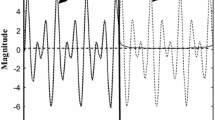
In this paper, a method of estimating the power spectrum of a complex signal based on the Group Delay function (GD) is proposed and also applied to the Wigner-Ville Distribution (WVD) to reduce the ripple effect due to the truncation of the autocorrelation sequence. The proposed method is realised by the GD for a complex signal and the modified GD concept. This extends the performance advantages of the modified GD applicable to a real signal, to a complex one. Further, its application to WVD, reduces the truncation/ripple effect without sacrificing any frequency resolution, as nocommon window function is used. Significant improvement in performance, in terms of reduction in variance without any compromise on resolution and higher noise immunity, has been found over those of the periodogram and windowed WVD.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Cohen L 1989 Time-frequency distribution — A review.Proc. IEEE. 77: 941–981

    Article  Google Scholar 

  • Flandrin P 1984 Some features of time-frequency representation of multicomponent signals.Int. Conf. on Acoustics, Speech and Signal Processing, pp 41B.4.1–41B.4.4

  • Jeong J, Williams W J 1992 Kernel design with reduced interference distributions.IEEE Trans. Signal Process. 38: 402–412

    Article  Google Scholar 

  • Kay S M 1988Modern spectral estimation: Theory and application (Englewood Cliffs, NJ: Prentice Hall)

    MATH  Google Scholar 

  • Murthy H A, Yegnanarayana B 1991 Speech processing using group delay function.Signal Process. 22: 259–267

    Article  Google Scholar 

  • Picone J 1988 Spectrum estimation using an analytic signal representation.Signal Process. 15: 169–182

    Article  MathSciNet  Google Scholar 

  • Reddy G R, Rao V V 1987 Group delay functions for complex signals.Signal Process. 12: 5–15

    Article  Google Scholar 

  • Velez E F, Absher R G 1990 Spectral estimation based on the Wigner-Ville representation.Signal Process. 20: 325–346

    Article  MATH  Google Scholar 

  • Yegnanarayana B, Murthy H A 1992 Significance of group delay functions in spectrum estimation.IEEE Trans. Signal Process. 40: 2281–2289

    Article  MATH  Google Scholar 

  • Yegnanarayana B, Saikia D K, Krishnan T R 1984 Significance of group delay functions in signal reconstruction from spectral magnitude or phase.IEEE Trans. Acoustics, Speech Signal Process. ASSP-32: 610–623

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Centre for Communication and Signal Processing, Department of Electrical and Computer Engineering, Concordia University, 1455, De Maisonneuve Blvd. West, H3G 1M8, Montreal, Canada

    E I Plotkin

  2. Aerospace Electronics Division, National Aerospace Labs, 560 017, Bangalore, India

    M N S Swamy

Authors
  1. S V Narasimhan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. E I Plotkin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M N S Swamy
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Narasimhan, S.V., Plotkin, E.I. & Swamy, M.N.S. Power spectrum estimation of complex signals and its application to Wigner-Ville distribution: A group delay approach. Sadhana 23, 57–71 (1998). https://doi.org/10.1007/BF02747623

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02747623

Keywords

Search

Navigation