Summary
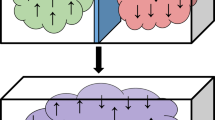
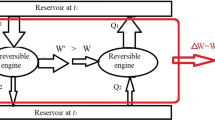
The problem of velocity selection by Maxwell’s demon in a many-particle gas, as distinct from a one-particle gas, is addressed. For such a situation it is shown that it is impossible to effect a separation of the molecules into two separate partitions so as to bring about an overall decrease in entropy unless information entropy is made available to the system. The validity of this conclusion is discussed in terms of the Gibbs paradox and the principle of quantum indistinguishability of identical particles.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
H. S. Leff andA. F. Rex:Maxwell’s Demon (Princeton University Press, Princeton, N.J., 1990).
H. S. Leff andA. F. Rex:Maxwell’s Demon (Princeton University Press, Princeton, N.J., 1990), p. 2.
R. Landauer:IBM J. Res. Dev.,5, 183 (1961).
C. H. Bennett:Int. J. Theor. Phys.,21, 905 (1982).
R. C. Tolman:The Principles of Statistical Mechanics (Oxford University Press, London, 1962), pp. 626–627.
L. E. Beghian:Nuovo Cimento B,107, 141 (1992).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Beghian, L.E. Maxwell’s demon revisited. Il Nuovo Cimento B 109, 611–616 (1994). https://doi.org/10.1007/BF02728444
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/BF02728444