On the shock-wave-generating function in a simple mixture of gases

Summary

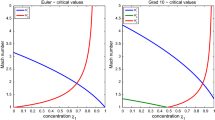
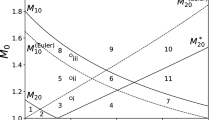
We present a study concerning the derivation of the so-called «shock generating function» in a flow of a simple mixture of ν ideal constituents. Due to the analytical complexity of this function, in general, numerical treatments have been discussed in some particular cases ( =2 and ν=3). On the basis of these results, we discovered that, unlike the classical model of a single fluid (where only the supersonic shock is admitted), the mutual interaction of the constituents of the mixture allows the rising of a new type ofk-shocks confined within intervals of low-shock Mach numbers, which satisfy the entropy principle. A procedure to symmetrize the system of the original balance equations in terms of the «main field» and the explicit computation of the jump of this field across the shock are also given in appendices.

Riassunto

Si calcola e si studia la cosiddetta «funzione generatrice dell’urto» in una miscela semplice di ν costituenti ideali. Essendo in generale tale funzione abbastanza complicata, si discutono alcuni modelli numerici nel caso particolare di fluidi composti da 2 o 3 costituenti. Sulla base di tali risultati si scopre che, a differenza di quanto accade nel caso classico di un singlo fluido (dove è ammesso il solo urto supersonico), la mutua interazione dei costituenti della miscela fa nascere un nuovo tipo dik-urti che soddisfano il principio di entropia in corrispondenza a limitati intervalli di piccoli numeri di Mach. Si riportano infine i procedimenti per simmetrizzare le equazioni originali di bilancio in funzione del «campo principale» e per costruire il salto di quest’ultimo attraverso l’urto.

Резюме

Мы исследуем вывод так называемой производящей функции ударных волн в потоке простой смеси ν идеальных компонент. Из-за аналитической сложности этой функции в общем случае, обсуждаются численные результаты для некоторых частных случаев (ν=2 и ν=3). На основе полученных результатов мы обнаружили, что в отличие от классической модели для одной среды (где может существовать только суперзвуковая ударная волна) взаимодействие компонент смеси допускает образование нового типаk ударных волн, в ограниченном интервале малых чисел Маха и которые удовлетворяют принципу энтропии. В приложении приводится процедура симметризации системы исходных уравнений баланса в терминах функий «главного поля» и явное вычисление скачка этого поля через ударную волну.